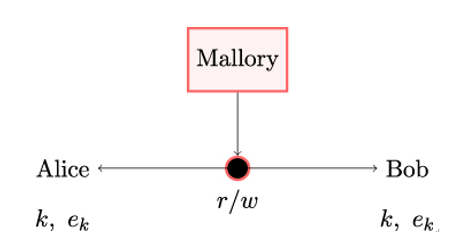
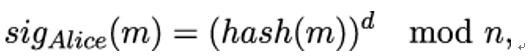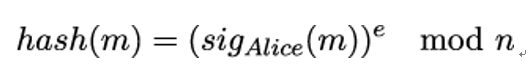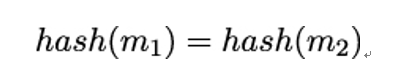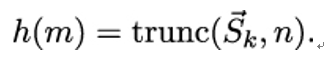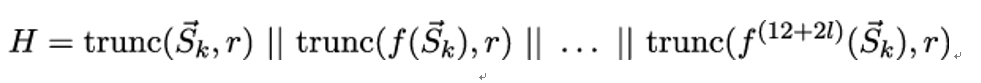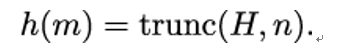10.2.6 X.509 trust model

Generally speaking, there are three steps in verifying a certificate:

• Verify that the certificate has not been revoked
• Verify that the certificate is valid (for instance, verify the certificate’s extensions and its validity period)
• Verify the signature of the CA over the certificate

As discussed earlier, the first step consists of either consulting a CRL or an OCSP server. But to verify the signature over a certificate (or a CRL or an OCSP response), we need an authentic copy of the CA’s public key – in other words, we need another certificate, in which the original CA is the subject. In X.509, these CA certificates are issued by a higher-order CA, which in turn has a certificate from an even higher-order CA, so that a hierarchical tree structure emerges with a Root CA at the top, which certifies itself (see Figure 10.4).

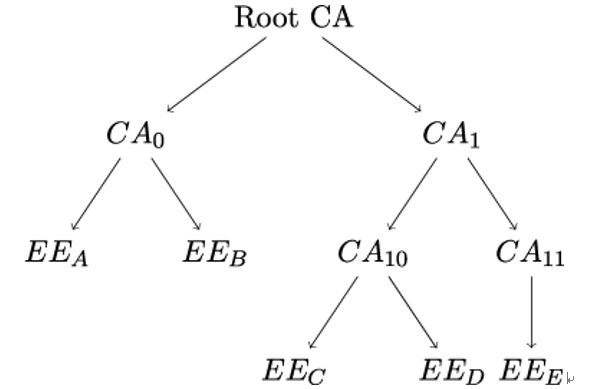
Figure 10.4: X.509 hierarchical trust model. An arrow from X to Y means that X certifies Y . EE stands for End Entity

The Path Length Constraint within the Basic Constraints extension field limits the number of CA certificates that may follow a CA certificate down the tree until the EE certificate under consideration is reached. For CA0 in Figure 10.4, for example, the path length constraint could be set to 0, whereas for CA1, the path length constraint should be at least 1, lest verification of the end entity certificates for C,D, and E fails.

In practice, a CA is rarely certified by another, independent CA. Rather, there are instances within the same company that act as root CAs for their own intermediate CA instances. From a security perspective, this is equivalent to a CA self-signing its own public key. This means that, in most cases, the relying parties cannot transfer the question of whether to trust a particular CA to some independent higher-order instance, but must base their trust decisions entirely on the publicly available information about a CA, for example, the CPS. Although modern browsers contain lists of trusted CAs, it is not entirely clear how these lists come about, and they should be no substitute for making your own decisions.

10.5.5 Certificates and TLS authentication messages

Recall that at the end of the TLS 1.3 handshake, client Bob and server Alice exchange authentication messages shown in bold in Figure 10.7. The same set of messages is used whenever client Bob and server Alice perform certificate-based authentication (authentication based on a pre-shared key happens as a side effect of the key exchange).

Figure 10.7: Full TLS 1.3 handshake with authentication messsages shown in bold

The set of authentication messages is composed of the Certificate, CertificateVerify, and Finished messages, as shown in Listing 10.4. These messages are protected using keys derived from client˙handshake˙traffic˙secret and server˙handshake˙traffic˙secret. Upon receiving server Alice’s authentication messages, client Bob responds with his authentication messages.

Listing 10.4: Authentication messages in TLS handshake

enum {
   X509(0),
   OpenPGP_RESERVED(1),
   RawPublicKey(2),
   (255)
} CertificateType;

struct {
   select (certificate_type) {
       case RawPublicKey:
           /* From RFC 7250 ASN.1_subjectPublicKeyInfo */
           opaque ASN1_subjectPublicKeyInfo<1..2^24-1>;
       case X509:
           opaque cert_data<1..2^24-1>;
   };
   Extension extensions<0..2^16-1>;
} CertificateEntry;

struct {
   opaque certificate_request_context<0..2^8-1>;
   CertificateEntry certificate_list<0..2^24-1>;
} Certificate;

struct {
   SignatureScheme algorithm;
   opaque signature<0..2^16-1>;
} CertificateVerify;

struct {
   opaque verify_data[Hash.length];
} Finished;

The Certificate message contains either Alice’s or Bob’s certificate and any per-certificate extensions. This message is omitted by server Alice if certificate-based authentication is not used in that TLS session and by client Bob if Alice did not send the CertificateRequest message (which would indicate that Alice wants Bob to authenticate himself using his digital certificate).

The CertificateVerify message carries the digital signature over the entire TLS handshake. The signature is generated using the private key that corresponds to the public key in the respective Certificate message. As an example, the signature in Alice’s CertificateVerify message is generated using Alice’s private key. Alice’s corresponding public key is contained in the certificate that Alice sends to Bob in her Certificate message. If certificate-based authentication is not used, this message is omitted.

The Finished message contains a so-called Message Authentication Code (MAC) over the entire TLS handshake. We will cover message authentication codes in detail in the next chapter on Hash Functions and Message Authentication Codes. For now, it suffices to know that they can be used as cryptographically secure checksums.

With this, Alice and Bob use the Finished message to verify that all handshake messages sent by Bob were not manipulated en route and were indeed received by Alice, and vice versa. As a result, the Finished message provides key confirmation, binds the identities of Alice and Bob to the exchanged secret keys, and, if the pre-shared key mode is used, authenticates the TLS handshake.

More generally, the Finished message illustrates a best practice in the design of cryptographic protocols where at the end of the protocol, the communicating parties verify that they had the same view of their interaction, for example, that no other messages were received except those that were actually sent and that no messages were lost.

10.5.10 OID filters

Using the oid˙filters extension, server Alice can send client Bob a set of pairs (Object Identifier (OID), value) that Bob’s digital certificate should match. If Alice decides to do so, she sends the oid˙filters extension in her CertificateRequest message.

The structure of the oid˙filters extension is shown in Listing 10.7. The filters variable holds a list of certificate extension OIDs with their corresponding values as defined in RFC 5280 Internet X.509 Public Key Infrastructure Certificate and Certificate Revocation List (CRL) Profile.

Listing 10.7: Structure of the oid_filters extension

struct {
   opaque certificate_extension_oid<1..2^8-1>;
   opaque certificate_extension_values<0..2^16-1>;
} OIDFilter;

struct {
   OIDFilter filters<0..2^16-1>;
} OIDFilterExtension;

If server Alice sends client Bob a non-empty oid˙filters extension, the certificate included in Bob’s response must contain all specified extension OIDs that Bob recognizes.

All specified values must be present in server Bob’s certificate for every extension OID that Bob is able to recognize. According to the TLS 1.3 specification, Bob must ignore any unrecognized certificate extension OID.

If client Bob ignores some of the required certificate extension OIDs and, as a result, the certificate that Bob presents to server Alice does not satisfy her request, Alice may either continue with the TLS handshake without appropriate certificate-based client authentication or terminate the TLS handshake and transmit the unsupported˙certificate alert.

10.5.11 Receiving a Certificate message

TLS endpoints have to follow certain rules when validating digital certificates. If client Bob receives an empty Certificate message from server Alice, Bob must immediately terminate the TLS handshake and send the decode˙error alert.

If, on the other hand, client Bob sends an empty Certificate message to server Alice, Alice is free to decide whether she continues the TLS handshake without proper authentication of client Bob—or, more precisely, a party claiming to be Bob—or terminates the TLS handshake and sends the certificate˙required alert.

Moreover, if the certificate chain received from client Bob is flawed—as an example, if it is not signed by a certification authority that Alice knows and trusts—Alice may continue or terminate the TLS handshake as she prefers.

If Alice or Bob receives a certificate that they would need to validate using any signature algorithm that uses the insecure MD5 hash function, they must immediately terminate the TLS handshake and send the bad˙certificate alert. The TLS 1.3 specification recommends Alice and Bob do the same if they receive a certificate that must be verified using a SHA-1 based signature algorithm.

Instead, the TLS 1.3 specification recommends all TLS endpoints transition to signature algorithms that use SHA-256 or stronger hash functions. In addition, TLS 1.3 allows a digital certificate that contains a key for one signature algorithm to be signed with a different signature algorithm.

11.1 The need for authenticity and integrity

Imagine Alice being a control computer in a train control system and Bob being a board computer installed within a train. For a more realistic scenario, let’s assume the train control system is a positive train control. This means that the train is only allowed to move if it receives an explicit move message from the train control. Otherwise, the train does not move.

Further, assume that there are two different move messages that onboard computer Bob can receive from control computer Alice:

• Message ms instructing the train to move slowly, for example, before entering a train station
• Message mf instructing the train to move fast

In addition, to secure the train control against cyberattacks, the communication channel between Alice and Bob is protected using a cryptographic mechanism that provides confidentiality only. That is, Alice and Bob share a secret key k and can compute an encryption function ek to make their communication unintelligible to the attacker, Mallory. However, they have no means to detect manipulation of the encrypted messages. The setup is illustrated in Figure 11.1.

Now, while Mallory cannot read the clear text communication between Alice and Bob, she can record and manipulate the encrypted messages. So, when Alice sends Bob the message ek(mf), Mallory simply changes it to the message ek(ms). Upon receiving the manipulated message, Bob decrypts it and obtains ms. Because ms is a legitimate message in the train control system, the onboard computer Bob accepts it and makes the train go slower than it is supposed to go, resulting in a delay at the next train station.

In cryptographic terms, the above attack works because Bob cannot verify the integrity of the message he received. After decrypting the message, Bob can determine whether it is in principle a valid train control message, but he has no way to check if it was manipulated en route.

Figure 11.1: Example setting ensuring confidentiality, but not integrity and authenticity

Next, imagine a scenario where the train is halted for safety reasons, say, waiting for another train coming from the opposite direction to pass. Since our example is a positive train control, no messages are sent by the control computer Alice to the onboard computer Bob and, as a result, the train remains halted. What happens if Mallory sends the message ek(ms) to Bob?

Upon receiving ek(ms), Bob decrypts it and obtains the clear text message ms telling the train to move slowly. Again, ms is a valid message in the train control system and so is processed by onboard computer Bob. The train is set in motion and, as a result, causes an accident if there is no human operator in the loop to react in a timely way.

From the cryptographic perspective, the above attack is possible because Bob cannot verify the authenticity of the received message ek(ms). While he can check that the plain text message ms is a valid message, Bob cannot determine whether it was actually sent by Alice or by someone else. In other words, Bob is not able to verify the origin of the message. Moreover, there is no way for Bob to verify the freshness of the message, which opens up further attack possibilities for Mallory (this was already discussed earlier, in Section 2.5, Authentication in Chapter 2, Secure Channel and the CIA Triad).

11.3 One-way functions

In Chapter 4, Encryption and Decryption, we learned that the notion of computational security is built on the concept of pseudorandomness, the idea that bit strings can look completely random even though they are not. In fact, pseudorandom generators, functions, and permutations form the basis of modern symmetric key cryptography. As being one-way is also one of the defining properties of a cryptographic hash function, we chose to include a more formal discussion of this property in this section, even though it is fundamental for the whole of cryptography.

This is because mathematicians have proved that pseudorandom generators, functions, and permutations can be constructed from one-way functions.

As a result, the existence of one-way functions is equivalent to the existence of any non-trivial symmetric-key cryptography [97]. This means, if we can find functions that we can prove to be one-way, we can use them to construct symmetric-key cryptographic schemes, for example, symmetric-key encryption algorithms or keyed hash functions, that are provably computationally secure.

The good news is that there is a number of functions mathematicians have studied for decades that exhibit one-way properties. We will cover some of the most prominent examples of such candidate one-way functions in a minute.

The bad news is that the currently known candidate one-way functions are much less efficient than constructions actually used in practice, say a modern block cipher. Bridging this gap between theory and practice is one of the most important open research problems in modern cryptography as it allows you to build provably-secure pseudorandom generators, functions, and permutations.

11.3.1 Mathematical properties

A function f : X → Y is called a one-way function if f(x) is easy to compute for all x ∈ X, but for essentially all elements y ∈ Y it is computationally infeasible to find any x ∈ X such that f(x) = y [117]. Such an x is called a preimage of y.

Here, easy to compute simply means that for any given x ∈ X, Alice and Bob can compute f(x) in polynomial time.

The requirement that it is computationally infeasible for Eve to find any x ∈ X such that f(x) = y means that a one-way function must be hard to invert. Since modern cryptography is about specifying cryptographic algorithms that are secure against a probabilistic polynomial-time attacker – to put it more precisely, that can be broken by a probabilistic polynomial-time attacker with only negligible probability – a function f is considered hard to invert if no probabilistic polynomial-time algorithm is capable of finding a preimage x ∈ X for any given element y ∈ Y , except with negligible probability.

The definition of what it means for a function to be hard to invert might seem complicated at first. But it actually only excludes two extremes:

• It is always possible to guess a preimage x. Since we can choose the size of the range of f, that is, the set {y = f(x) ∈ Y |x ∈ X}, when designing a cryptographic algorithm, we can make the likelihood of a successful guess arbitrarily small, but never zero. As a result, we need to account for the fact that Eve could find a preimage y for a randomly chosen x with negligible probability.
• It is always possible to find a preimage of y by brute-force searching the domain of f(x), that is, by simply trying all values of x until one produces the correct y. Such a brute-force search requires exponential time. As a result, we exclude this extreme by requiring f to be computationally infeasible to invert only for probabilistic polynomial-time algorithms.

Summing up, a function y = f(x) is said to be one-way, if it is hard to invert for all values of y. If there is a probabilistic polynomial-time algorithm that can invert f for some values of y with a non-negligible probability—even if this probability is very small—then f is not a one-way function.

Because the brute-force search runs in exponential time and always succeeds, the existence of one-way functions is an assumption about computational complexity and computational hardness [97]. In other words, it is an assumption about the existence of mathematical problems that can be solved in principle, but cannot be solved efficiently.

11.4 Hash functions

A hash function is some function hash that maps an arbitrarily long input string onto an output string of fixed length n. More formally, we have hash : {0,1}∗→{0,1}n.

A simplistic example of a hash function would be a function that always outputs the last n bits of an arbitrary input string m. Or, if n = 1, one could use the bitwise XOR of all input bits as the hash value.

However, these simple hash functions do not possess any of the properties required from a cryptographically secure hash function. We will now first discuss these properties, and afterward look at how secure hash functions are actually constructed.

11.4.1 Collision resistance

Cryptographic hash functions are hard to construct because they have to fulfill stringent requirements, which are motivated by their use within Message Authentication Codes (MACs) (see Section 11.5, Message Authentication Codes) and Digital Signatures (see Chapter 9, Digital Signatures).

Recall, for example, that in the RSA cryptosystem, Alice computes a digital signature over some message m as

where d is Alice’s private key and n is the public module. Alice then sends the pair (m,sigAlice(m)) to Bob.

If Eve observes this pair, she can compute hash(m) using Alice’s public key PKAlice = (e,n) via

Eve now knows hash(m) and the corresponding preimage m. If she manages to find another message m with the same hash value (a so-called second preimage), m and m will have the same signature. Effectively, Eve has signed m in Alice’s name without knowing her private key. This is the most severe kind of attack on a cryptographic hash function.

Therefore, given m and hash(m), it must be computationally hard for Eve to find a second preimage m such that hash(m) = hash(m). This property of a cryptographic hash function is called second preimage resistance or weak collision resistance.

Note that when trying out different input messages for the hash function, collisions must occur at some point, because hash can map longer messages onto shorter messages. In particular, if the given hash value hash(m) is n bits long, a second preimage m should be found after O(2n) trials. Therefore a second preimage attack is considered successful only if it has a significantly smaller complexity than O(2n).

A weaker form of attack occurs if Eve manages to find any collision, that is, any two messages m1,m2 with

without reference to some given hash value. If it is computationally hard for Eve to construct any collisions, the hash is called strongly collision resistant.

Again, when trying out many different candidate messages, collisions will naturally occur at some point, this time after about 2n∕2 trials. This smaller number is a consequence of a phenomenon commonly known as Birthday Paradox, which we will discuss in detail in Section 19.7, Attacks on hash functions in Chapter 19, Attacks on Cryptography.

Consequently, an attack on strong collision resistance is considered successful only if it has a significantly smaller complexity than O(2n∕2). This also shows that in general, that is, assuming there are no cryptographic weaknesses, hash functions with longer hash values can be considered to be more secure than hash functions with shorter hash values.

Note that strong collision resistance of a hash function implies weak collision resistance. Hash functions that are both strongly and weakly collision resistant are called collision resistant hash functions (CRHF).

11.4.4 Sponge construction

Sponge construction is used in the formulation of the SHA-3 standard hash algorithm Keccak [26]. It works by first absorbing the input message into some state vector →S (the sponge). After one block has been absorbed, the state vector is permuted to achieve a good mixing of the input bits. After all input blocks have been processed, the n bits of the hash value are squeezed out of the sponge.

The detailed construction is as follows:

1. Separate message m into k blocks of length r.
2. Form the first state vector →S0 = 0b, that is, a string consisting of b 0’s, where b = 25 × 2l, and b > r.
3. Absorb: For each message block, modify state vector →Si−1 by message block mi and permute the result via some bijective round function f : {0,1}b → 0,1b:

The final result is a b-bit vector →Sk, into which the message blocks have been absorbed.

4. Squeeze: We are now squeezing n bit out of the state vector →Sk.

If n < r, we simply take the first n bit of →Sk:

Otherwise, we form the following string of length (12 + 2l + 1) × r by repeatedly applying the round function f on →Sk:

Afterward, we pick the first n bits again:

We will now see how hash functions are used to form Message Authentication Codes (MACs).

11.5 Message authentication codes

If Alice wants to securely transmit a message m to Bob, she must use a so-called Message Authentication Code (MAC) to prevent Eve from tampering with that message. More precisely, a MAC prevents Mallory from doing the following:

• Modifying m without Bob noticing it
• Presenting Bob a message m′ generated by Mallory, m′≠m, without Bob noticing that m′ was not sent by Alice

Therefore, a MAC helps us to achieve the two security objectives integrity protection and message authentication (see Chapter 2, Secure Channel and the CIA Triad and Chapter 5, Entity Authentication). Note that a MAC cannot prevent the tampering itself, nor can it prevent message replay. The active attacker Mallory can always manipulate the genuine message m, or present Bob with the message m′ and pretend that it was sent by Alice. A MAC only gives Bob the ability to detect that something went wrong during the transmission of the message he received. Bob cannot reconstruct the genuine message m from a MAC. In fact, he cannot even determine whether the wrong MAC results from an attack by Mallory or from an innocuous bit flip caused by a transmission error. Later in this chapter, we will see that this property has fundamental implications on the use of MACs in safety-critical systems.

If Alice and Bob want to secure their messages with MACs, they need to share a secret k in advance. Once the shared secret is established, Alice and Bob can use MACs as illustrated in Figure 11.2. The sender Alice computes the MAC t as a function of her message m and the secret key k she shares with Bob. She then appends t to message m—denoted by m∥t—and sends the result to Bob. Upon receiving the data, Bob uses the message m, the MAC t, and the shared secret k to verify that t is a valid MAC on message m.

Figure 11.2: Working principle of MACs

So how are MACs actually computed?

So, to encode a two-byte message 0x0102, Bob would interpret it as the polynomial m(x) = x8 + x, divide it by x2 + x + 1 using polynomial division, and get a remainder polynomial r(x) = 1. In hexadecimal notation, the remainder has the value 0x01. He would then append the remainder value as the CRC check value and transmit the message 0x010201 to Alice.

Upon receiving the message, Alice would perform the same computation and check whether the received CRC value 0x01 is equal to the computed CRC value. Let’s assume there was an error during transmission – an accidental bit flip – so that Alice received the message 0x010101. In that case, the CRC value computed by Alice would be 0x02 and Alice would detect the transmission error.

At first glance, this looks very similar to a MAC and, especially in systems that already support CRCs, it might be tempting to use CRC as a replacement for a MAC. Don’t! Recall that MACs are built on top of cryptographic hash functions, and cryptographic hash functions are collision-resistant. CRCs, on the other hand, are not collision resistant.

As an example, Listing 11.1 shows the Python code for computing CRC-8. This CRC uses generator polynomial x2 + x + 1 and outputs an 8-bit CRC value.

Listing 11.1: Python code for computing CRC-8 using generator polynomial x2+x+1

def crc8(data, n, poly, crc=0):
   g = 1 << n | poly  # Generator polynomial
   for d in data:
       crc ^= d << (n – 8)
       for _ in range(8):
           crc <<= 1
           if crc & (1 << n):
               crc ^= g
   return crc

Now, if you compute CRC-8 checksum values for different 2-byte messages using the code shown in Listing 11.2, you can quickly verify yourself that messages 0x020B, 0x030C, 0x0419, and many others have the same CRC value of 0x1B.

Listing 11.2: Python code to compute CRC-8 for different 2-byte messages

for i in range(0,256):
   for j in range(0, 256):
       if crc8([i,j], 8, 0x07) == 0x1b:
           print(f”Message {hex(i)}, {hex(j)} has CRC 0x1b”)

Consequently, if Alice and Bob were to use CRCs to protect their message integrity against malicious attacker Mallory rather than accidental transmission errors, it would be very easy for Mallory to find messages that have an identical CRC check value. That, in turn, would allow Mallory to exchange a message that Bob sent to Alice without her noticing it (and vice versa). And that is exactly the reason why a MAC needs to be collision-resistant. Moreover, and maybe even more importantly, even if Mallory cannot be bothered to find collisions for the CRC value already in place, he can simply compute the matching CRC value for a message of his choice and replace both the message and the CRC. This is possible because there is no secret information going into the CRC. To summarize, a CRC will only protect you against accidental, random transmission errors, but not against an intelligent attacker.

Setting the initial hash value

Before the actual hash computation can begin, the initial hash value H0 must be set based on the specific hash algorithm used. For SHA-256, H(0) is composed of the following 8 32-bit words – denoted H0(0) to H7(0) – which are the first 32 bits of the fractional parts of the square roots of the first 8 prime numbers:

H0(0) = 6a09e667

H1(0) = bb67ae85

H2(0) = 3c6ef372

H3(0) = a54ff53a

H4(0) = 510e527f

H5(0) = 9b05688c

H6(0) = 1f83d9ab

H7(0) = 5be0cd19

For SHA-384, H(0) is composed of eight 64-bit words denoted H0(0) to H7(0), the words being the first 64 bits of the fractional parts of the square roots of the ninth through sixteenth prime numbers:

H0(0) = cbbb9d5dc1059ed8

H1(0) = 629a292a367cd507

H2(0) = 9159015a3070dd17

H3(0) = 152fecd8f70e5939

H4(0) = 67332667ffc00b31

H5(0) = 8eb44a8768581511

H6(0) = db0c2e0d64f98fa7

H7(0) = 47b5481dbefa4fa4

For SHA-512, H(0) is composed of the 8 64-bit words – denoted H0(0) to H7(0) – which are the first 64 bits of the fractional parts of the square roots of the first 8 prime numbers:

H0(0) = 6a09e667f3bcc908

H1(0) = bb67ae8584caa73b

H2(0) = 3c6ef372fe94f82b

H3(0) = a54ff53a5f1d36f1

H4(0) = 510e527fade682d1

H5(0) = 9b05688c2b3e6c1f

H6(0) = 1f83d9abfb41bd6b

H7(0) = 5be0cd19137e2179

The way the constants for the initial hash value H(0) were chosen for the SHA-2 family hash algorithms – namely, by taking the first 16 prime numbers, computing a square root of these numbers, and taking the first 32 or 64 bits of the fractional part of these square roots – is yet another example of nothing-up-my-sleeve numbers.

Because prime numbers are the atoms of number theory and the square root is a simple, well-known operation, it is very unlikely that these constants were chosen for any specific reason.

The choice of the constants is natural and their values are limited because only the first 16 prime numbers are used. As a result, it is very unlikely that someone could design a cryptographic hash function containing a backdoor based on these constants.

Message digest computation

Recall that for SHA-256, the message is first padded to have a length that is a multiple of 512. To compute the SHA-256 message digest, the message is parsed into N 512-bit blocks M(1),M(2),…M(N) is processed as shown in Algorithm 1.

The term Mt(i) denotes specific 32 bits of the 512-bit block M(i). As an example, M0(i) denotes the first 32 bits of block M(i), M1(i) denotes the next 32 bits of block M(i), and so on, up to M15(i). Moreover, the SHA-256 algorithm uses a so-called message schedule consisting of 64 32-bit words W0 to W63, 8 32-bit working variables a to h, and 2 temporary variables T1,T2. The algorithm outputs a 256-bit hash value composed of 8 32-bit words.

Computation of the SHA-512 message digest, shown in Algorithm 2, is identical to that of SHA-256, except that the message schedule consists of 80 64-bit words W0 to W79 and the algorithm uses 8 64-bit working variables a to h and outputs a 512-bit message digest composed of 8 64-bit words.

Moreover, the term Mt(i) now denotes specific 64 bits of the 1,024-bit block M(i). That is, M0(i) denotes the first 64 bits of block M(i), M1(i) denotes the next 64 bits of block M(i), and so on, up to M15(i).

Finally, the SHA-384 hash algorithm is computed exactly like SHA-512, except the following:

• The initial hash value H(0) for SHA-384 is used
• The final hash value H(N) is truncated to H0(N)|| H1(N)|| H2(N)|| H3(N)|| H4(N)|| H5(N) to produce a 384-bit message digest

Algorithm 1: Computation of the SHA-256 message digest.

Algorithm 2: Computation of the SHA-512 message digest

SHA-256, SHA-384, and SHA-512 hash functions

SHA-256, SHA-384, and SHA-512 are hash algorithms from the Secure Hash Algorithm-2 (SHA-2) family. The algorithms are defined in FIPS 180-4, Secure Hash Standard (SHS) [129], the standard specifying NIST-approved hash algorithms for generating message digests, and are based on the Merkle-Damgard construction.

The suffix of the SHA-2 algorithms denotes the length of the message digest in bits [140]. As an example, the message digest of SHA-256 has a length of 256 bits. Table 11.1 summarizes the message size, block size, and digest size of all SHA-2 hash family algorithms.

Algorithm.	Message size (bits)	Block size (bits)	Digest size (bits)
SHA-1	< 264	512	160
SHA-224	< 264	512	224
SHA-256	< 264	512	256
SHA-384	< 2128	1024	384
SHA-512	< 2128	1024	512
SHA-512/224	< 2128	1024	224
SHA-512/256	< 2128	1024	256

 Table 11.1: Basic properties of SHA-2 hash family algorithms

All SHA-2 hash algorithms use a set of similar basic functions, only with different lengths of input and output. Every SHA-2 algorithm uses the following functions where x,y, and z are either 32-bit or 64-bit values, ⊕ denotes exclusive-OR, and ∧ denotes bitwise AND:

• Ch(x,y,z) = (x ∧ y) ⊕ (¬x ∧ z)
• Maj(x,y,z) = (x ∧ y) ⊕ (x ∧ z) ⊕ (y ∧ z)

SHA-256 functions

In addition to the preceding functions, SHA-256 uses four logical functions. Each function is applied to a 32-bit value x and outputs a 32-bit result:

∑ 0256(x) = ROTR2(x) ⊕ ROTR13(x) ⊕ ROTR22(x)

∑ 1256(x) = ROTR6(x) ⊕ ROTR11(x) ⊕ ROTR25(x)

σ0256(x) = ROTR7(x) ⊕ ROTR18(x) ⊕ SHR3(x)

σ1256(x) = ROTR17(x) ⊕ ROTR19(x) ⊕ SHR10(x)

In the preceding functions, ROTRn(x) denotes a circular right-shift operation applied to a w-bit word x, using an integer 0 ≤ n < w, defined as (x ≫ n) ∨ (x ≪ w −n), and SHRn(x) denotes a right-shift operation applied to a w-bit word x, using an integer 0 ≤ n < w, defined as x ≫ n.

SHA-512 functions

Similar to SHA-256, SHA-384 and SHA-512 also use four logical functions. However, the functions are applied to a 64-bit value x and output a 64-bit result:

∑ 0512(x) = ROTR28(x) ⊕ ROTR34(x) ⊕ ROTR39(x)

∑ 1512(x) = ROTR14(x) ⊕ ROTR18(x) ⊕ ROTR41(x)

σ0512(x) = ROTR1(x) ⊕ ROTR8(x) ⊕ SHR7(x)

σ1512(x) = ROTR19(x) ⊕ ROTR61(x) ⊕ SHR6(x)

SHA-256 constants

SHA-256 uses 64 32-bit constants K0256,K1256,…,K63256 that are the first 32 bits of the fractional parts of cube roots of the first 64 prime numbers.

SHA-384 and SHA-512 constants

SHA-384 and SHA-512 use 80 64-bit constants K0512,K1512,…,K79512 that are the first 64 bits of the fractional parts of cube roots of the first 80 prime numbers.

Preprocessing the message

All hash functions in the SHA-2 family preprocess the message before performing the actual computation. The preprocessing consists of three steps:

1. Padding the plaintext message to obtain a padded message that is a multiple of 512 bits for SHA-256 and a multiple of 1,024 bits for SHA-384 and SHA-512.
2. Parsing the message into blocks.
3. Setting the initial hash value H(0).

For SHA-256, the padded message is parsed into N 512-bit blocks M1,M2,…,MN. Because every 512-bit input block can be divided into 16 32-bit words, the input block i can be expressed as M0i,M1i,…,M1i5 where every Mji has the length of 32 bits.

Similarly, for SHA-384 and SHA-512, the padded message is parsed into N 1,024-bit blocks M1,M2,…MN. Because a 1024-bit input block can be divided into 16 64-bit words, the input block i can be expressed as M0i,M1i,…,M1i5 where every Mji has the length of 64 bits.