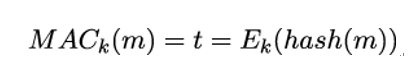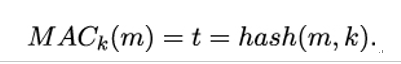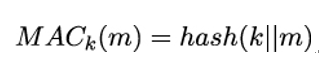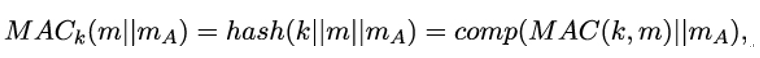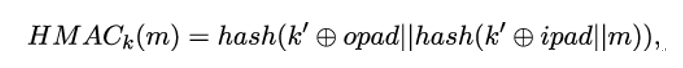11.3.2 Candidate one-way functions

With the current knowledge in complexity theory, mathematicians do not know how to unconditionally prove the existence of one-way functions. As a result, their existence can only be assumed. There are, however, good reasons to make this assumption: there exists a number of very natural computational problems that were the subject of intense mathematical research for decades, sometimes even centuries, yet no one was able to come up with a polynomial-time algorithm that can solve these problems.

According to the fundamental theorem of arithmetic, every positive integer can be expressed as a product of prime numbers, the numbers being referred to as prime factors of the original number [74]. One of the best known computational problems that is believed to be a one-way function is prime factorization: given a large integer, find its prime factors.

The first table of prime factors of integers was created by the Greek mathematician Eratosthenes more than 2,500 years ago. The last factor table for numbers up to 10,017,000 was published by the American mathematician Derrick Norman Lehmer in 1909 [178].

Trial division was first described in 1202 by Leonardo of Pisa, also known as Fibonacci, in his manuscript on arithmetic Liber Abaci. French mathematician Pierre de Fermat proposed a method based on a difference of squares, today known as Fermat’s factorization method, in the 17th century. A similar integer factorization method was described by the 14th century Indian mathematician Narayana Pandita. The 18th century Swiss mathematician Leonhard Euler proposed a method for factoring integers by writing them as a sum of two square numbers in two different ways.

Starting from the 1970s, a number of so-called algebraic-group factorization algorithms were introduced that work in an algebraic group. As an example, the British mathematician John Pollard introduced two new factoring algorithms called the p− 1 algorithm and the rho algorithm in 1974 and 1975, respectively. The Canadian mathematician Hugh Williams proposed the Williams’ p + 1 algorithm in 1982.

In 1985, the Dutch mathematician Hendrik Lenstra published the elliptic curve method, currently the best known integer factorization method among the algorithms whose complexity depends on the size of the factor rather than the size of the number to be factored [204].

Moreover, a number of so-called general-purpose integer factorization methods whose running time depends on the size of the number to be factored have been proposed over time. Examples of such algorithms are the Quadratic Sieve introduced in 1981 by the American mathematician Carl Pomerance, which was the most effective general-purpose algorithm in the 1980s and early 1990s, and the General Number Field Sieve method, the fastest currently known algorithm for factoring large integers [39].

Yet, except for the quantum computer algorithm proposed in 1994 by the American mathematician Peter Shor, none of the above algorithms can factor integers in polynomial time. As a result, mathematicians assume that prime factorization is indeed a one-way function, at least for classical computers. Shor’s algorithm, on the other hand, requires a sufficiently large quantum computer with advanced error correction capabilities to keep the qubits stable during the entire computation, a technical challenge for which no solutions are known as of today.

Another example of a function believed to be one-way is a family of permutations based on the discrete logarithm problem. Recall that the discrete logarithm problem involves determining the integer exponent x given a number of the form gx where g is a generator of a cyclic group. The problem is believed to be computationally intractable, that is, no algorithms are known that can solve this problem in polynomial time.

The conjectured one-way family of permutations consists of the following:

• An algorithm to generate an n-bit prime p and an element g ∈ {2,…,p − 1}
• An algorithm to generate a random integer x in the range {1,…,p−1}
• The function fp,g(x) = gx (mod p)

Function fp,g(x) is easy to compute, for example, using the square-and-multiply algorithm. Inverting fp,g(x), on the other hand, is believed to be computationally hard because inverting modular exponentiation is equivalent to solving the discrete logarithm problem for which no polynomial-time algorithms are known to date, as discussed in Chapter 7, Public-Key Cryptography.

11.4 Hash functions

A hash function is some function hash that maps an arbitrarily long input string onto an output string of fixed length n. More formally, we have hash : {0,1}∗→{0,1}n.

A simplistic example of a hash function would be a function that always outputs the last n bits of an arbitrary input string m. Or, if n = 1, one could use the bitwise XOR of all input bits as the hash value.

However, these simple hash functions do not possess any of the properties required from a cryptographically secure hash function. We will now first discuss these properties, and afterward look at how secure hash functions are actually constructed.

11.4.1 Collision resistance

Cryptographic hash functions are hard to construct because they have to fulfill stringent requirements, which are motivated by their use within Message Authentication Codes (MACs) (see Section 11.5, Message Authentication Codes) and Digital Signatures (see Chapter 9, Digital Signatures).

Recall, for example, that in the RSA cryptosystem, Alice computes a digital signature over some message m as

where d is Alice’s private key and n is the public module. Alice then sends the pair (m,sigAlice(m)) to Bob.

If Eve observes this pair, she can compute hash(m) using Alice’s public key PKAlice = (e,n) via

Eve now knows hash(m) and the corresponding preimage m. If she manages to find another message m with the same hash value (a so-called second preimage), m and m will have the same signature. Effectively, Eve has signed m in Alice’s name without knowing her private key. This is the most severe kind of attack on a cryptographic hash function.

Therefore, given m and hash(m), it must be computationally hard for Eve to find a second preimage m such that hash(m) = hash(m). This property of a cryptographic hash function is called second preimage resistance or weak collision resistance.

Note that when trying out different input messages for the hash function, collisions must occur at some point, because hash can map longer messages onto shorter messages. In particular, if the given hash value hash(m) is n bits long, a second preimage m should be found after O(2n) trials. Therefore a second preimage attack is considered successful only if it has a significantly smaller complexity than O(2n).

A weaker form of attack occurs if Eve manages to find any collision, that is, any two messages m1,m2 with

without reference to some given hash value. If it is computationally hard for Eve to construct any collisions, the hash is called strongly collision resistant.

Again, when trying out many different candidate messages, collisions will naturally occur at some point, this time after about 2n∕2 trials. This smaller number is a consequence of a phenomenon commonly known as Birthday Paradox, which we will discuss in detail in Section 19.7, Attacks on hash functions in Chapter 19, Attacks on Cryptography.

Consequently, an attack on strong collision resistance is considered successful only if it has a significantly smaller complexity than O(2n∕2). This also shows that in general, that is, assuming there are no cryptographic weaknesses, hash functions with longer hash values can be considered to be more secure than hash functions with shorter hash values.

Note that strong collision resistance of a hash function implies weak collision resistance. Hash functions that are both strongly and weakly collision resistant are called collision resistant hash functions (CRHF).

11.4.2 One-way property

In Chapter 5, Entity Authentication, we showed how passwords can be stored in a secure way on a server using hash functions. More specifically, each password is hashed together with some random value (the salt) and the hash value is stored together with the corresponding user ID. This system can only be secure if it is computationally difficult to invert the hash function, that is, to find a matching input for a known output. The same requirement emerges if the hash function is used in a key-dependent way in order to form a MAC (see Section 11.5, Message authentication codes).

In order to put this requirement in a more precise way, we only need to apply our earlier definition of a one-way function from Section 11.3, One-way functions, to hash functions:

A hash function hash is said to be one-way or preimage resistant, if it is computationally infeasible to find an input m for a given output y so that y = hash(m).

As is the case for second preimages, preimages for a given n-bit output will occur automatically after O(2n) trial inputs. Hash functions that are preimage resistant and second preimage resistant are called one-way hash functions (OWHF).

11.4.3 Merkle-Damgard construction

Our previous discussion of requirements on a secure hash function shows that in order to achieve collision resistance, it is important that all input bits have an influence on the hash value. Otherwise, it would be very easy to construct collisions by varying the input bits that do not influence the outcome.

How can we accommodate this requirement when dealing with inputs m of indeterminate length? We divide m into pieces (or blocks) of a fixed size, then you deal with the blocks one after the other. In one construction option, the block is compressed, that is mapped onto a smaller bit string, which is then processed together with the next block.

The Merkle-Damgard scheme has been the main construction principle for cryptographic hash functions in the past. Most importantly, the MD5 (128-bit hash), SHA-1 (160-bit hash), and SHA-2 (256-bit hash) hash functions are built according to this scheme. Later in this chapter, in Section 11.7, Hash functions in TLS, we will look at the SHA-family of hash functions in detail, as these functions play an important role within TLS.

For now, we’ll concentrate on the details of the Merkle-Damgard scheme. In order to compute the hash value of an input message m of arbitrary length, we proceed according to the following steps:

• Separate message m into k blocks of length r, using padding if necessary. In the SHA-1 hash function, input messages are always padded by a 1 followed by the necessary number of 0-bits. The block length of SHA-1 is r = 512.
• Concatenate the first block m1 with an initialization vector IV of length n.
• Apply a compression function comp : {0,1}n+r → {0,1}n on the result, to get

• Process the remaining blocks by computing

Note that each hi has length n.

• Set

Note that finding a collision in comp implies a collision in hash. More precisely, if we can find two different bit strings y1,y2 of length r so that comp(x||y1) = comp(x||y2) for some given n−bit string x, then we can construct two different messages m,m with the same hash value:

The article [8] lists a number of generic attacks on hash functions based on the Merkle-Damgard scheme. Although in most cases these attacks are far from being practical, they are still reason for concern about the general security of the scheme.

11.4.4 Sponge construction

Sponge construction is used in the formulation of the SHA-3 standard hash algorithm Keccak [26]. It works by first absorbing the input message into some state vector →S (the sponge). After one block has been absorbed, the state vector is permuted to achieve a good mixing of the input bits. After all input blocks have been processed, the n bits of the hash value are squeezed out of the sponge.

The detailed construction is as follows:

1. Separate message m into k blocks of length r.
2. Form the first state vector →S0 = 0b, that is, a string consisting of b 0’s, where b = 25 × 2l, and b > r.
3. Absorb: For each message block, modify state vector →Si−1 by message block mi and permute the result via some bijective round function f : {0,1}b → 0,1b:

The final result is a b-bit vector →Sk, into which the message blocks have been absorbed.

4. Squeeze: We are now squeezing n bit out of the state vector →Sk.

If n < r, we simply take the first n bit of →Sk:

Otherwise, we form the following string of length (12 + 2l + 1) × r by repeatedly applying the round function f on →Sk:

Afterward, we pick the first n bits again:

We will now see how hash functions are used to form Message Authentication Codes (MACs).

11.5 Message authentication codes

If Alice wants to securely transmit a message m to Bob, she must use a so-called Message Authentication Code (MAC) to prevent Eve from tampering with that message. More precisely, a MAC prevents Mallory from doing the following:

• Modifying m without Bob noticing it
• Presenting Bob a message m′ generated by Mallory, m′≠m, without Bob noticing that m′ was not sent by Alice

Therefore, a MAC helps us to achieve the two security objectives integrity protection and message authentication (see Chapter 2, Secure Channel and the CIA Triad and Chapter 5, Entity Authentication). Note that a MAC cannot prevent the tampering itself, nor can it prevent message replay. The active attacker Mallory can always manipulate the genuine message m, or present Bob with the message m′ and pretend that it was sent by Alice. A MAC only gives Bob the ability to detect that something went wrong during the transmission of the message he received. Bob cannot reconstruct the genuine message m from a MAC. In fact, he cannot even determine whether the wrong MAC results from an attack by Mallory or from an innocuous bit flip caused by a transmission error. Later in this chapter, we will see that this property has fundamental implications on the use of MACs in safety-critical systems.

If Alice and Bob want to secure their messages with MACs, they need to share a secret k in advance. Once the shared secret is established, Alice and Bob can use MACs as illustrated in Figure 11.2. The sender Alice computes the MAC t as a function of her message m and the secret key k she shares with Bob. She then appends t to message m—denoted by m∥t—and sends the result to Bob. Upon receiving the data, Bob uses the message m, the MAC t, and the shared secret k to verify that t is a valid MAC on message m.

Figure 11.2: Working principle of MACs

So how are MACs actually computed?

11.5.1 How to compute a MAC

Basically, there are two options to form a MAC. The first option closely follows the approach we adopted to compute digital signatures in Chapter 9, Digital Signatures. Back then, we hashed the message m first and encrypted the hash value with the signer’s private key:

Analogously, using their shared secret k, Alice and Bob could compute

as MAC. Here, encryption is done via some symmetric encryption function, for example, a block cipher (see Chapter 14, Block Ciphers and Their Modes of Operation). Note that if Alice sends m||t to Bob and Eve manages to find another message m so that hash(m) = hash(m), then Eve can replace m with m without being noticed. This motivates the collision resistance requirement on hash functions described in Section 11.4, Hash functions.

However, even if we are using a collision-resistant hash function, in a symmetric setting where Alice and Bob both use the same key k, one might ask whether it is really necessary to agree on and deploy two different kinds of algorithms for computing a MAC. Moreover, hash functions are built for speed and generally have a much better performance than block ciphers.

The second option for computing a MAC therefore only uses hash functions as building blocks. Here, the secret k is used to modify the message m in a certain way and the hash function is applied to the result:

This option is called a key-dependent hash value. In which way k should influence the message m, depends on how the hash function is constructed. In any case, if Eve is able to reconstruct the input data from the output value hash(m,k), she might be able to get part of or even the complete secret key k. This motivates the one-way property requirement on hash functions described in Section 11.4, Hash functions. A well-proven way to construct a key-dependent hash called HMAC is defined in [103].

11.5.2 HMAC construction

The HMAC construction is a generic template for constructing a MAC via a key-dependent hash function. In this construction, the underlying hash function hash is treated as a black box that can be easily replaced by some other hash function if necessary. This construction also makes it easy to use existing implementations of hash functions. It is used within TLS as part of the key derivation function HKDF (see Section 12.3, Key derivation functions in TLS within Chapter 12, Key Exchange).

When looking at the way hash functions are built, using either the Merkle-Damgard or the Sponge Construction, it quickly becomes clear that input bits from the first message blocks are well diffused over the final output hash value. Input bits in the last message blocks, on the other hand, are only processed at the very end and the compression or the round function, respectively, is only applied a few times on these bits. It is therefore a good idea to always append the message to the key in key-dependent hash functions. The simple construction

however, suffers from so-called Hash Length Extension Attacks, if the hash function is constructed according to the Merkle-Damgard scheme. Here, an attacker knowing a valid pair (m,MACk(m)) can append another message mA to the original message m and compute the corresponding MAC without knowing the secret key k. This is because

where comp is the compression function used for building the hash function.

In the HMAC construction, the input message m is therefore appended twice to the keying material, but the second time in a hashed form that cannot be forged by an attacker. More specifically, for an input message m and a symmetric key k, we have

where:

• hash : {0,1}∗ → {0,1}n is some collision-resistant OWHF, which processes its input in blocks of size r.
• k is the symmetric key. It is recommended that the key size should be ≥ n. If k has more than r bits, one should use hash(k) instead of k.
• k′ is the key padded with zeros so that the result has r bits.
• opad and ipad are fixed bitstrings of length r: opad = 01011100 repeated r∕8 times, and ipad = 00110110 repeated r∕8 times. Both opad and ipad, when added via ⊕, flip half of the key bits.

In this construction, the hash length extension attack will not work, because in order to forge MACk(m||mA), an attacker would need to construct hash(k′⊕ ipad||m||mA). This is impossible, however, as the attacker does not know hash(k′⊕ ipad||m).

More generally, the HMAC construction does not rely on the collision-resistance of the underlying hash function, because a collision in the hash function does not imply the construction of a colliding HMAC.

So, to encode a two-byte message 0x0102, Bob would interpret it as the polynomial m(x) = x8 + x, divide it by x2 + x + 1 using polynomial division, and get a remainder polynomial r(x) = 1. In hexadecimal notation, the remainder has the value 0x01. He would then append the remainder value as the CRC check value and transmit the message 0x010201 to Alice.

Upon receiving the message, Alice would perform the same computation and check whether the received CRC value 0x01 is equal to the computed CRC value. Let’s assume there was an error during transmission – an accidental bit flip – so that Alice received the message 0x010101. In that case, the CRC value computed by Alice would be 0x02 and Alice would detect the transmission error.

At first glance, this looks very similar to a MAC and, especially in systems that already support CRCs, it might be tempting to use CRC as a replacement for a MAC. Don’t! Recall that MACs are built on top of cryptographic hash functions, and cryptographic hash functions are collision-resistant. CRCs, on the other hand, are not collision resistant.

As an example, Listing 11.1 shows the Python code for computing CRC-8. This CRC uses generator polynomial x2 + x + 1 and outputs an 8-bit CRC value.

Listing 11.1: Python code for computing CRC-8 using generator polynomial x2+x+1

def crc8(data, n, poly, crc=0):
   g = 1 << n | poly  # Generator polynomial
   for d in data:
       crc ^= d << (n – 8)
       for _ in range(8):
           crc <<= 1
           if crc & (1 << n):
               crc ^= g
   return crc

Now, if you compute CRC-8 checksum values for different 2-byte messages using the code shown in Listing 11.2, you can quickly verify yourself that messages 0x020B, 0x030C, 0x0419, and many others have the same CRC value of 0x1B.

Listing 11.2: Python code to compute CRC-8 for different 2-byte messages

for i in range(0,256):
   for j in range(0, 256):
       if crc8([i,j], 8, 0x07) == 0x1b:
           print(f”Message {hex(i)}, {hex(j)} has CRC 0x1b”)

Consequently, if Alice and Bob were to use CRCs to protect their message integrity against malicious attacker Mallory rather than accidental transmission errors, it would be very easy for Mallory to find messages that have an identical CRC check value. That, in turn, would allow Mallory to exchange a message that Bob sent to Alice without her noticing it (and vice versa). And that is exactly the reason why a MAC needs to be collision-resistant. Moreover, and maybe even more importantly, even if Mallory cannot be bothered to find collisions for the CRC value already in place, he can simply compute the matching CRC value for a message of his choice and replace both the message and the CRC. This is possible because there is no secret information going into the CRC. To summarize, a CRC will only protect you against accidental, random transmission errors, but not against an intelligent attacker.

11.6 MAC versus CRC

Can we construct a MAC without a cryptographic hash function and without a secret key? Let’s take a look at the Cyclic Redundancy Check (CRC), which is popular error-detecting code used in communication systems to detect accidental errors in messages sent over a noisy or unreliable communication channel.

The working principle of error-detecting code is for the sender to encode their plaintext message in a redundant way. The redundancy, in turn, allows the receiver to detect a certain number of errors – that is, accidental bit flips – in the message they receive. The theory of channel coding, pioneered in the 1940s by the American mathematician Richard Hamming, aims to find code that has minimal overhead (that is, the least redundancy) but, at the same time, has a large number of valid code words and can correct or detect many errors.

CRC is so-called cyclic code, that is, a block code where a circular shift of every code word yields another valid code word. The use of cyclic code for error detection in communication systems was first proposed by the American mathematician and computer scientist Wesley Peterson in 1961.

Cyclic code encodes the plaintext message by attaching to it a fixed-length check value based on the remainder of a polynomial division of the message’s content. The receiving party repeats that calculation and checks whether the received check value is equal to the computed check value.

The algebraic properties of cyclic code make it suitable for efficient error detection and correction. Cyclic code is simple to implement and well suited to detect so-called burst errors. Burst errors are contiguous sequences of erroneous bits in communication messages and are common in many real-world communication channels.

CRC code is defined using a generator polynomial g(x) with binary coefficients 0 and 1. The plaintext message, encoded as another polynomial m(x), is divided by the generator polynomial. The CRC is then computed by discarding the resulting quotient polynomial and taking the remainder polynomial r(x) as CRC, which is subsequently appended to the plaintext as a checksum. The whole arithmetic is done within the finite field 𝔽2, therefore the coefficients of the remainder polynomial are also 0 and 1.

As an example, we can compute an 8-bit CRC using the generator polynomial g(x) = x2 + x + 1. To encode a message, we encode it as a polynomial, divide it by the generator polynomial x2 + x + 1, and take the remainder of this division as the CRC check value to be appended to the plaintext message.

Setting the initial hash value

Before the actual hash computation can begin, the initial hash value H0 must be set based on the specific hash algorithm used. For SHA-256, H(0) is composed of the following 8 32-bit words – denoted H0(0) to H7(0) – which are the first 32 bits of the fractional parts of the square roots of the first 8 prime numbers:

H0(0) = 6a09e667

H1(0) = bb67ae85

H2(0) = 3c6ef372

H3(0) = a54ff53a

H4(0) = 510e527f

H5(0) = 9b05688c

H6(0) = 1f83d9ab

H7(0) = 5be0cd19

For SHA-384, H(0) is composed of eight 64-bit words denoted H0(0) to H7(0), the words being the first 64 bits of the fractional parts of the square roots of the ninth through sixteenth prime numbers:

H0(0) = cbbb9d5dc1059ed8

H1(0) = 629a292a367cd507

H2(0) = 9159015a3070dd17

H3(0) = 152fecd8f70e5939

H4(0) = 67332667ffc00b31

H5(0) = 8eb44a8768581511

H6(0) = db0c2e0d64f98fa7

H7(0) = 47b5481dbefa4fa4

For SHA-512, H(0) is composed of the 8 64-bit words – denoted H0(0) to H7(0) – which are the first 64 bits of the fractional parts of the square roots of the first 8 prime numbers:

H0(0) = 6a09e667f3bcc908

H1(0) = bb67ae8584caa73b

H2(0) = 3c6ef372fe94f82b

H3(0) = a54ff53a5f1d36f1

H4(0) = 510e527fade682d1

H5(0) = 9b05688c2b3e6c1f

H6(0) = 1f83d9abfb41bd6b

H7(0) = 5be0cd19137e2179

The way the constants for the initial hash value H(0) were chosen for the SHA-2 family hash algorithms – namely, by taking the first 16 prime numbers, computing a square root of these numbers, and taking the first 32 or 64 bits of the fractional part of these square roots – is yet another example of nothing-up-my-sleeve numbers.

Because prime numbers are the atoms of number theory and the square root is a simple, well-known operation, it is very unlikely that these constants were chosen for any specific reason.

The choice of the constants is natural and their values are limited because only the first 16 prime numbers are used. As a result, it is very unlikely that someone could design a cryptographic hash function containing a backdoor based on these constants.

Message digest computation

Recall that for SHA-256, the message is first padded to have a length that is a multiple of 512. To compute the SHA-256 message digest, the message is parsed into N 512-bit blocks M(1),M(2),…M(N) is processed as shown in Algorithm 1.

The term Mt(i) denotes specific 32 bits of the 512-bit block M(i). As an example, M0(i) denotes the first 32 bits of block M(i), M1(i) denotes the next 32 bits of block M(i), and so on, up to M15(i). Moreover, the SHA-256 algorithm uses a so-called message schedule consisting of 64 32-bit words W0 to W63, 8 32-bit working variables a to h, and 2 temporary variables T1,T2. The algorithm outputs a 256-bit hash value composed of 8 32-bit words.

Computation of the SHA-512 message digest, shown in Algorithm 2, is identical to that of SHA-256, except that the message schedule consists of 80 64-bit words W0 to W79 and the algorithm uses 8 64-bit working variables a to h and outputs a 512-bit message digest composed of 8 64-bit words.

Moreover, the term Mt(i) now denotes specific 64 bits of the 1,024-bit block M(i). That is, M0(i) denotes the first 64 bits of block M(i), M1(i) denotes the next 64 bits of block M(i), and so on, up to M15(i).

Finally, the SHA-384 hash algorithm is computed exactly like SHA-512, except the following:

• The initial hash value H(0) for SHA-384 is used
• The final hash value H(N) is truncated to H0(N)|| H1(N)|| H2(N)|| H3(N)|| H4(N)|| H5(N) to produce a 384-bit message digest

Algorithm 1: Computation of the SHA-256 message digest.

Algorithm 2: Computation of the SHA-512 message digest

SHA-256, SHA-384, and SHA-512 hash functions

SHA-256, SHA-384, and SHA-512 are hash algorithms from the Secure Hash Algorithm-2 (SHA-2) family. The algorithms are defined in FIPS 180-4, Secure Hash Standard (SHS) [129], the standard specifying NIST-approved hash algorithms for generating message digests, and are based on the Merkle-Damgard construction.

The suffix of the SHA-2 algorithms denotes the length of the message digest in bits [140]. As an example, the message digest of SHA-256 has a length of 256 bits. Table 11.1 summarizes the message size, block size, and digest size of all SHA-2 hash family algorithms.

Algorithm.	Message size (bits)	Block size (bits)	Digest size (bits)
SHA-1	< 264	512	160
SHA-224	< 264	512	224
SHA-256	< 264	512	256
SHA-384	< 2128	1024	384
SHA-512	< 2128	1024	512
SHA-512/224	< 2128	1024	224
SHA-512/256	< 2128	1024	256

 Table 11.1: Basic properties of SHA-2 hash family algorithms

All SHA-2 hash algorithms use a set of similar basic functions, only with different lengths of input and output. Every SHA-2 algorithm uses the following functions where x,y, and z are either 32-bit or 64-bit values, ⊕ denotes exclusive-OR, and ∧ denotes bitwise AND:

• Ch(x,y,z) = (x ∧ y) ⊕ (¬x ∧ z)
• Maj(x,y,z) = (x ∧ y) ⊕ (x ∧ z) ⊕ (y ∧ z)

SHA-256 functions

In addition to the preceding functions, SHA-256 uses four logical functions. Each function is applied to a 32-bit value x and outputs a 32-bit result:

∑ 0256(x) = ROTR2(x) ⊕ ROTR13(x) ⊕ ROTR22(x)

∑ 1256(x) = ROTR6(x) ⊕ ROTR11(x) ⊕ ROTR25(x)

σ0256(x) = ROTR7(x) ⊕ ROTR18(x) ⊕ SHR3(x)

σ1256(x) = ROTR17(x) ⊕ ROTR19(x) ⊕ SHR10(x)

In the preceding functions, ROTRn(x) denotes a circular right-shift operation applied to a w-bit word x, using an integer 0 ≤ n < w, defined as (x ≫ n) ∨ (x ≪ w −n), and SHRn(x) denotes a right-shift operation applied to a w-bit word x, using an integer 0 ≤ n < w, defined as x ≫ n.

SHA-512 functions

Similar to SHA-256, SHA-384 and SHA-512 also use four logical functions. However, the functions are applied to a 64-bit value x and output a 64-bit result:

∑ 0512(x) = ROTR28(x) ⊕ ROTR34(x) ⊕ ROTR39(x)

∑ 1512(x) = ROTR14(x) ⊕ ROTR18(x) ⊕ ROTR41(x)

σ0512(x) = ROTR1(x) ⊕ ROTR8(x) ⊕ SHR7(x)

σ1512(x) = ROTR19(x) ⊕ ROTR61(x) ⊕ SHR6(x)

SHA-256 constants

SHA-256 uses 64 32-bit constants K0256,K1256,…,K63256 that are the first 32 bits of the fractional parts of cube roots of the first 64 prime numbers.

SHA-384 and SHA-512 constants

SHA-384 and SHA-512 use 80 64-bit constants K0512,K1512,…,K79512 that are the first 64 bits of the fractional parts of cube roots of the first 80 prime numbers.

Preprocessing the message

All hash functions in the SHA-2 family preprocess the message before performing the actual computation. The preprocessing consists of three steps:

1. Padding the plaintext message to obtain a padded message that is a multiple of 512 bits for SHA-256 and a multiple of 1,024 bits for SHA-384 and SHA-512.
2. Parsing the message into blocks.
3. Setting the initial hash value H(0).

For SHA-256, the padded message is parsed into N 512-bit blocks M1,M2,…,MN. Because every 512-bit input block can be divided into 16 32-bit words, the input block i can be expressed as M0i,M1i,…,M1i5 where every Mji has the length of 32 bits.

Similarly, for SHA-384 and SHA-512, the padded message is parsed into N 1,024-bit blocks M1,M2,…MN. Because a 1024-bit input block can be divided into 16 64-bit words, the input block i can be expressed as M0i,M1i,…,M1i5 where every Mji has the length of 64 bits.

11.7 Hash functions in TLS 1.3

We’ll now take a look at how hash functions are negotiated within the TLS handshake and how they are subsequently used in the handshake.

11.7.1 Hash functions in ClientHello

Recall that Alice and Rob use the TLS handshake protocol to negotiate the security parameters for their connection. They do it using TLS handshake messages shown in Listing 11.3. Once assembled by the TLS endpoint – that is, server Alice or client Bob – these messages are passed to the TLS record layer where they are embedded into one or more TLSPlaintext or TLSCiphertext data structures. The data structures are then transmitted according to the current state of the TLS connection.

Listing 11.3: TLS 1.3 handshake messages

enum {
   client_hello(1),
   server_hello(2),
   new_session_ticket(4),
   end_of_early_data(5),
   encrypted_extensions(8),
   certificate(11),
   certificate_request(13),
   certificate_verify(15),
   finished(20),
   key_update(24),
   message_hash(254),
   (255)
} HandshakeType;

One of the most important TLS handshake messages is ClientHello since this message starts a TLS session between client Bob and server Alice. The structure of the ClientHello message is shown in Listing 11.4. The cipher˙suites field in ClientHello carries a list of symmetric key algorithms supported by client Bob, specifically the encryption algorithm protecting the TLS record layer and the hash function used with the HMAC-based key derivation function HKDF.

Listing 11.4: TLS 1.3 ClientHello message

struct {
   ProtocolVersion legacy_version = 0x0303;    /* TLS v1.2 */
   Random random;
   opaque legacy_session_id<0..32>;
   CipherSuite cipher_suites<2..2^16-2>;
   opaque legacy_compression_methods<1..2^8-1>;
   Extension extensions<8..2^16-1>;
} ClientHello;

11.7.2 Hash Functions in TLS 1.3 signature schemes

Recall that server Alice and client Bob also agree upon the signature scheme they will use during the TLS handshake. The SignatureScheme field indicates the signature algorithm with the corresponding hash function. The following code shows digital signature schemes supported in TLS 1.3:

enum {
    /* RSASSA-PKCS1-v1_5 algorithms */
    rsa_pkcs1_sha256(0x0401),
    rsa_pkcs1_sha384(0x0501),
    rsa_pkcs1_sha512(0x0601),
    /* ECDSA algorithms */
    ecdsa_secp256r1_sha256(0x0403),
    ecdsa_secp384r1_sha384(0x0503),
    ecdsa_secp521r1_sha512(0x0603),
    /* RSASSA-PSS algorithms with public key OID rsaEncryption */
    rsa_pss_rsae_sha256(0x0804),
    rsa_pss_rsae_sha384(0x0805),
    rsa_pss_rsae_sha512(0x0806),
    /* EdDSA algorithms */
    ed25519(0x0807),
    ed448(0x0808),
    /* RSASSA-PSS algorithms with public key OID RSASSA-PSS */
    rsa_pss_pss_sha256(0x0809),
    rsa_pss_pss_sha384(0x080a),
    rsa_pss_pss_sha512(0x080b),
    — snip —
} SignatureScheme;

We’ll now discuss the SHA family of hash functions in detail.

SHA-1

SHA-1 is a hash algorithm that was in use from 1995 as part of the FIPS standard 180-1, but has been deprecated by NIST, BSI, and other agencies due to severe security issues with regard to its collision resistance. In 2005, a team of Chinese researchers published the first cryptanalytic attacks against the SHA-1 algorithm. These theoretical attacks allowed the researchers to find collisions with much less work than with a brute-force attack. Following further improvements in these attacks, NIST deprecated SHA-1 in 2011 and disallowed using it for digital signatures in 2013.

In 2017, a team of researchers from the CWI Institute in Amsterdam and Google published Shattered, the first practical attack on SHA-1, by crafting two different PDF files having an identical SHA-1 signature. You can test the attack yourself at https://shattered.io/.

Finally, in 2020, two French researchers published the first practical chosen-prefix collision attack against SHA-1. Using the attack, Mallory can build colliding messages with two arbitrary prefixes. This is much more threatening for cryptographic protocols, and the researchers have demonstrated their work by mounting a PGP/GnuPG impersonation attack. Moreover, the cost of computing such chosen-prefix collisions has been significantly reduced over time and is now considered to be within the reach of attackers with computing resources similar to those of academic researchers [64].

While SHA-1 must not be used as a secure cryptographic hash function, it may still be used in other cryptographic applications [64]. As an example, based on what is known today, SHA-1 can be used for HMAC because the HMAC construction does not require collision resistance. Nevertheless, authorities recommend replacing SHA-1 with a hash function from the SHA-2 or SHA-3 family as an additional security measure [64].