12.3.3 HKDF-Expand-Label
HKDF-Expand-Label (or HEL for short) is a pseudorandom function as shown in Figure 12.5. Recall this means that it can be efficiently computed for any given input, but it cannot be efficiently distinguished from a uniformly random function [37].
HKDF-Expand-Label takes a secret, the desired length of the output L, and an HKDF-Label as input, and expands them to OKM.
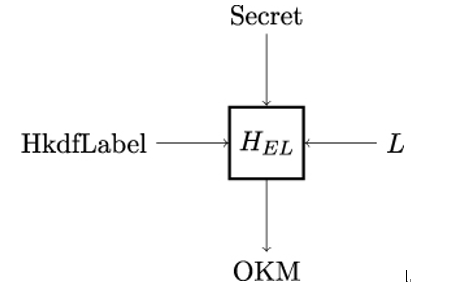
Figure 12.5: The HKDF-Expand-Label function HEL
The HkdfLabel data structure is defined as in Listing 12.1. It essentially consists of a label and a context. All labels used in TLS 1.3 are strings. The context might have zero length.
Listing 12.1: HkdfLabel data structure
struct {
uint16 length = Length;
opaque label<7..255> = “tls13 ” + Label;
opaque context<0..255> = Context;
} HkdfLabel;
HKDF-Expand-Label illustrates a cryptographic good practice where keying material and, in turn, keys are derived for a specific purpose using a label and a context as inputs to the KDF.
12.3.4 Derive-Secret
Finally, the TLS 1.3 Derive-Secret function DS is defined as shown in Figure 12.6. It takes a secret, a label, and TLS messages as input, and outputs one of the TLS secrets listed in Table 12.1. In the subsequent step, these secrets will be used to derive the TLS keys.
As a result, multiple calls to Derive-Secret can be used to derive keying material for different secret keys even with the same secret as input as long as different messages are used to compute the transcript hash.
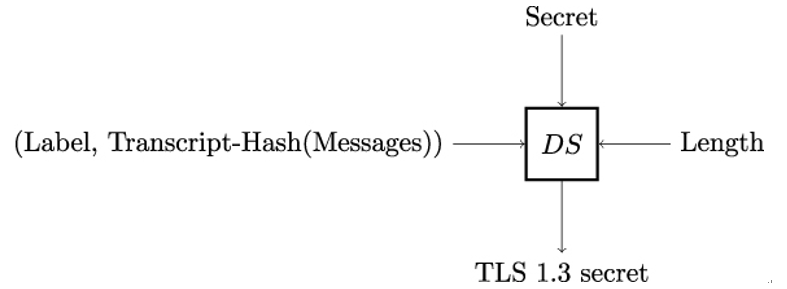
Figure 12.6: The Derive-Secret function DS
Derive-Secret implements a clever way to bind the keying material to previous messages exchanged during a specific execution of a cryptographic protocol. This is desirable from a cryptography perspective because it causes Alice and Bob to derive completely different secret keys and, as a result, leads to a failure of the cryptographic protocol since Alice cannot understand what Bob encrypted or authenticated, and vice versa.
This approach implements an implicit protection against man-in-the-middle attacks. Even if Mallory manages to intercept and manipulate messages exchanged by Alice and Bob, she cannot trick them into deriving an identical secret key because Alice’s message transcript will be different from Bob’s message transcript.
As illustrated in Figure 12.7, Alice and Bob start by deriving the Early Secret SE and an intermediate secret S0 (which will be used for further computations). Eventually, Alice and Bob will establish a secure TLS channel by deriving the shared cryptographic keys from these secrets.
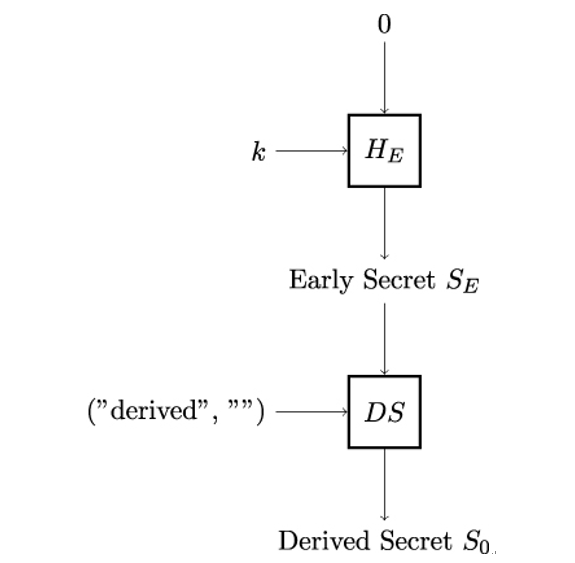
Figure 12.7: Derivation of the TLS early secret and first derived secret S0
If a specific TLS secret is not available, a zero value – a string of 0-valued bytes – is taken as input. As an example, if the pre-shared key PSK is not used, the early secret will be computed as follows:
Early_Secret = HKDF-Extract(0, 0)