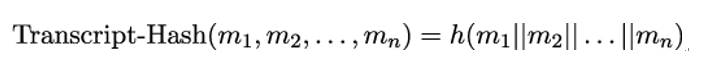11.6 MAC versus CRC

Can we construct a MAC without a cryptographic hash function and without a secret key? Let’s take a look at the Cyclic Redundancy Check (CRC), which is popular error-detecting code used in communication systems to detect accidental errors in messages sent over a noisy or unreliable communication channel.

The working principle of error-detecting code is for the sender to encode their plaintext message in a redundant way. The redundancy, in turn, allows the receiver to detect a certain number of errors – that is, accidental bit flips – in the message they receive. The theory of channel coding, pioneered in the 1940s by the American mathematician Richard Hamming, aims to find code that has minimal overhead (that is, the least redundancy) but, at the same time, has a large number of valid code words and can correct or detect many errors.

CRC is so-called cyclic code, that is, a block code where a circular shift of every code word yields another valid code word. The use of cyclic code for error detection in communication systems was first proposed by the American mathematician and computer scientist Wesley Peterson in 1961.

Cyclic code encodes the plaintext message by attaching to it a fixed-length check value based on the remainder of a polynomial division of the message’s content. The receiving party repeats that calculation and checks whether the received check value is equal to the computed check value.

The algebraic properties of cyclic code make it suitable for efficient error detection and correction. Cyclic code is simple to implement and well suited to detect so-called burst errors. Burst errors are contiguous sequences of erroneous bits in communication messages and are common in many real-world communication channels.

CRC code is defined using a generator polynomial g(x) with binary coefficients 0 and 1. The plaintext message, encoded as another polynomial m(x), is divided by the generator polynomial. The CRC is then computed by discarding the resulting quotient polynomial and taking the remainder polynomial r(x) as CRC, which is subsequently appended to the plaintext as a checksum. The whole arithmetic is done within the finite field 𝔽2, therefore the coefficients of the remainder polynomial are also 0 and 1.

As an example, we can compute an 8-bit CRC using the generator polynomial g(x) = x2 + x + 1. To encode a message, we encode it as a polynomial, divide it by the generator polynomial x2 + x + 1, and take the remainder of this division as the CRC check value to be appended to the plaintext message.

Setting the initial hash value

Before the actual hash computation can begin, the initial hash value H0 must be set based on the specific hash algorithm used. For SHA-256, H(0) is composed of the following 8 32-bit words – denoted H0(0) to H7(0) – which are the first 32 bits of the fractional parts of the square roots of the first 8 prime numbers:

H0(0) = 6a09e667

H1(0) = bb67ae85

H2(0) = 3c6ef372

H3(0) = a54ff53a

H4(0) = 510e527f

H5(0) = 9b05688c

H6(0) = 1f83d9ab

H7(0) = 5be0cd19

For SHA-384, H(0) is composed of eight 64-bit words denoted H0(0) to H7(0), the words being the first 64 bits of the fractional parts of the square roots of the ninth through sixteenth prime numbers:

H0(0) = cbbb9d5dc1059ed8

H1(0) = 629a292a367cd507

H2(0) = 9159015a3070dd17

H3(0) = 152fecd8f70e5939

H4(0) = 67332667ffc00b31

H5(0) = 8eb44a8768581511

H6(0) = db0c2e0d64f98fa7

H7(0) = 47b5481dbefa4fa4

For SHA-512, H(0) is composed of the 8 64-bit words – denoted H0(0) to H7(0) – which are the first 64 bits of the fractional parts of the square roots of the first 8 prime numbers:

H0(0) = 6a09e667f3bcc908

H1(0) = bb67ae8584caa73b

H2(0) = 3c6ef372fe94f82b

H3(0) = a54ff53a5f1d36f1

H4(0) = 510e527fade682d1

H5(0) = 9b05688c2b3e6c1f

H6(0) = 1f83d9abfb41bd6b

H7(0) = 5be0cd19137e2179

The way the constants for the initial hash value H(0) were chosen for the SHA-2 family hash algorithms – namely, by taking the first 16 prime numbers, computing a square root of these numbers, and taking the first 32 or 64 bits of the fractional part of these square roots – is yet another example of nothing-up-my-sleeve numbers.

Because prime numbers are the atoms of number theory and the square root is a simple, well-known operation, it is very unlikely that these constants were chosen for any specific reason.

The choice of the constants is natural and their values are limited because only the first 16 prime numbers are used. As a result, it is very unlikely that someone could design a cryptographic hash function containing a backdoor based on these constants.

Message digest computation

Recall that for SHA-256, the message is first padded to have a length that is a multiple of 512. To compute the SHA-256 message digest, the message is parsed into N 512-bit blocks M(1),M(2),…M(N) is processed as shown in Algorithm 1.

The term Mt(i) denotes specific 32 bits of the 512-bit block M(i). As an example, M0(i) denotes the first 32 bits of block M(i), M1(i) denotes the next 32 bits of block M(i), and so on, up to M15(i). Moreover, the SHA-256 algorithm uses a so-called message schedule consisting of 64 32-bit words W0 to W63, 8 32-bit working variables a to h, and 2 temporary variables T1,T2. The algorithm outputs a 256-bit hash value composed of 8 32-bit words.

Computation of the SHA-512 message digest, shown in Algorithm 2, is identical to that of SHA-256, except that the message schedule consists of 80 64-bit words W0 to W79 and the algorithm uses 8 64-bit working variables a to h and outputs a 512-bit message digest composed of 8 64-bit words.

Moreover, the term Mt(i) now denotes specific 64 bits of the 1,024-bit block M(i). That is, M0(i) denotes the first 64 bits of block M(i), M1(i) denotes the next 64 bits of block M(i), and so on, up to M15(i).

Finally, the SHA-384 hash algorithm is computed exactly like SHA-512, except the following:

• The initial hash value H(0) for SHA-384 is used
• The final hash value H(N) is truncated to H0(N)|| H1(N)|| H2(N)|| H3(N)|| H4(N)|| H5(N) to produce a 384-bit message digest

Algorithm 1: Computation of the SHA-256 message digest.

Algorithm 2: Computation of the SHA-512 message digest

SHA-256, SHA-384, and SHA-512 hash functions

SHA-256, SHA-384, and SHA-512 are hash algorithms from the Secure Hash Algorithm-2 (SHA-2) family. The algorithms are defined in FIPS 180-4, Secure Hash Standard (SHS) [129], the standard specifying NIST-approved hash algorithms for generating message digests, and are based on the Merkle-Damgard construction.

The suffix of the SHA-2 algorithms denotes the length of the message digest in bits [140]. As an example, the message digest of SHA-256 has a length of 256 bits. Table 11.1 summarizes the message size, block size, and digest size of all SHA-2 hash family algorithms.

Algorithm.	Message size (bits)	Block size (bits)	Digest size (bits)
SHA-1	< 264	512	160
SHA-224	< 264	512	224
SHA-256	< 264	512	256
SHA-384	< 2128	1024	384
SHA-512	< 2128	1024	512
SHA-512/224	< 2128	1024	224
SHA-512/256	< 2128	1024	256

 Table 11.1: Basic properties of SHA-2 hash family algorithms

All SHA-2 hash algorithms use a set of similar basic functions, only with different lengths of input and output. Every SHA-2 algorithm uses the following functions where x,y, and z are either 32-bit or 64-bit values, ⊕ denotes exclusive-OR, and ∧ denotes bitwise AND:

• Ch(x,y,z) = (x ∧ y) ⊕ (¬x ∧ z)
• Maj(x,y,z) = (x ∧ y) ⊕ (x ∧ z) ⊕ (y ∧ z)

SHA-256 functions

In addition to the preceding functions, SHA-256 uses four logical functions. Each function is applied to a 32-bit value x and outputs a 32-bit result:

∑ 0256(x) = ROTR2(x) ⊕ ROTR13(x) ⊕ ROTR22(x)

∑ 1256(x) = ROTR6(x) ⊕ ROTR11(x) ⊕ ROTR25(x)

σ0256(x) = ROTR7(x) ⊕ ROTR18(x) ⊕ SHR3(x)

σ1256(x) = ROTR17(x) ⊕ ROTR19(x) ⊕ SHR10(x)

In the preceding functions, ROTRn(x) denotes a circular right-shift operation applied to a w-bit word x, using an integer 0 ≤ n < w, defined as (x ≫ n) ∨ (x ≪ w −n), and SHRn(x) denotes a right-shift operation applied to a w-bit word x, using an integer 0 ≤ n < w, defined as x ≫ n.

SHA-512 functions

Similar to SHA-256, SHA-384 and SHA-512 also use four logical functions. However, the functions are applied to a 64-bit value x and output a 64-bit result:

∑ 0512(x) = ROTR28(x) ⊕ ROTR34(x) ⊕ ROTR39(x)

∑ 1512(x) = ROTR14(x) ⊕ ROTR18(x) ⊕ ROTR41(x)

σ0512(x) = ROTR1(x) ⊕ ROTR8(x) ⊕ SHR7(x)

σ1512(x) = ROTR19(x) ⊕ ROTR61(x) ⊕ SHR6(x)

SHA-256 constants

SHA-256 uses 64 32-bit constants K0256,K1256,…,K63256 that are the first 32 bits of the fractional parts of cube roots of the first 64 prime numbers.

SHA-384 and SHA-512 constants

SHA-384 and SHA-512 use 80 64-bit constants K0512,K1512,…,K79512 that are the first 64 bits of the fractional parts of cube roots of the first 80 prime numbers.

Preprocessing the message

All hash functions in the SHA-2 family preprocess the message before performing the actual computation. The preprocessing consists of three steps:

1. Padding the plaintext message to obtain a padded message that is a multiple of 512 bits for SHA-256 and a multiple of 1,024 bits for SHA-384 and SHA-512.
2. Parsing the message into blocks.
3. Setting the initial hash value H(0).

For SHA-256, the padded message is parsed into N 512-bit blocks M1,M2,…,MN. Because every 512-bit input block can be divided into 16 32-bit words, the input block i can be expressed as M0i,M1i,…,M1i5 where every Mji has the length of 32 bits.

Similarly, for SHA-384 and SHA-512, the padded message is parsed into N 1,024-bit blocks M1,M2,…MN. Because a 1024-bit input block can be divided into 16 64-bit words, the input block i can be expressed as M0i,M1i,…,M1i5 where every Mji has the length of 64 bits.

11.7 Hash functions in TLS 1.3

We’ll now take a look at how hash functions are negotiated within the TLS handshake and how they are subsequently used in the handshake.

11.7.1 Hash functions in ClientHello

Recall that Alice and Rob use the TLS handshake protocol to negotiate the security parameters for their connection. They do it using TLS handshake messages shown in Listing 11.3. Once assembled by the TLS endpoint – that is, server Alice or client Bob – these messages are passed to the TLS record layer where they are embedded into one or more TLSPlaintext or TLSCiphertext data structures. The data structures are then transmitted according to the current state of the TLS connection.

Listing 11.3: TLS 1.3 handshake messages

enum {
   client_hello(1),
   server_hello(2),
   new_session_ticket(4),
   end_of_early_data(5),
   encrypted_extensions(8),
   certificate(11),
   certificate_request(13),
   certificate_verify(15),
   finished(20),
   key_update(24),
   message_hash(254),
   (255)
} HandshakeType;

One of the most important TLS handshake messages is ClientHello since this message starts a TLS session between client Bob and server Alice. The structure of the ClientHello message is shown in Listing 11.4. The cipher˙suites field in ClientHello carries a list of symmetric key algorithms supported by client Bob, specifically the encryption algorithm protecting the TLS record layer and the hash function used with the HMAC-based key derivation function HKDF.

Listing 11.4: TLS 1.3 ClientHello message

struct {
   ProtocolVersion legacy_version = 0x0303;    /* TLS v1.2 */
   Random random;
   opaque legacy_session_id<0..32>;
   CipherSuite cipher_suites<2..2^16-2>;
   opaque legacy_compression_methods<1..2^8-1>;
   Extension extensions<8..2^16-1>;
} ClientHello;

11.7.2 Hash Functions in TLS 1.3 signature schemes

Recall that server Alice and client Bob also agree upon the signature scheme they will use during the TLS handshake. The SignatureScheme field indicates the signature algorithm with the corresponding hash function. The following code shows digital signature schemes supported in TLS 1.3:

enum {
    /* RSASSA-PKCS1-v1_5 algorithms */
    rsa_pkcs1_sha256(0x0401),
    rsa_pkcs1_sha384(0x0501),
    rsa_pkcs1_sha512(0x0601),
    /* ECDSA algorithms */
    ecdsa_secp256r1_sha256(0x0403),
    ecdsa_secp384r1_sha384(0x0503),
    ecdsa_secp521r1_sha512(0x0603),
    /* RSASSA-PSS algorithms with public key OID rsaEncryption */
    rsa_pss_rsae_sha256(0x0804),
    rsa_pss_rsae_sha384(0x0805),
    rsa_pss_rsae_sha512(0x0806),
    /* EdDSA algorithms */
    ed25519(0x0807),
    ed448(0x0808),
    /* RSASSA-PSS algorithms with public key OID RSASSA-PSS */
    rsa_pss_pss_sha256(0x0809),
    rsa_pss_pss_sha384(0x080a),
    rsa_pss_pss_sha512(0x080b),
    — snip —
} SignatureScheme;

We’ll now discuss the SHA family of hash functions in detail.

SHA-1

SHA-1 is a hash algorithm that was in use from 1995 as part of the FIPS standard 180-1, but has been deprecated by NIST, BSI, and other agencies due to severe security issues with regard to its collision resistance. In 2005, a team of Chinese researchers published the first cryptanalytic attacks against the SHA-1 algorithm. These theoretical attacks allowed the researchers to find collisions with much less work than with a brute-force attack. Following further improvements in these attacks, NIST deprecated SHA-1 in 2011 and disallowed using it for digital signatures in 2013.

In 2017, a team of researchers from the CWI Institute in Amsterdam and Google published Shattered, the first practical attack on SHA-1, by crafting two different PDF files having an identical SHA-1 signature. You can test the attack yourself at https://shattered.io/.

Finally, in 2020, two French researchers published the first practical chosen-prefix collision attack against SHA-1. Using the attack, Mallory can build colliding messages with two arbitrary prefixes. This is much more threatening for cryptographic protocols, and the researchers have demonstrated their work by mounting a PGP/GnuPG impersonation attack. Moreover, the cost of computing such chosen-prefix collisions has been significantly reduced over time and is now considered to be within the reach of attackers with computing resources similar to those of academic researchers [64].

While SHA-1 must not be used as a secure cryptographic hash function, it may still be used in other cryptographic applications [64]. As an example, based on what is known today, SHA-1 can be used for HMAC because the HMAC construction does not require collision resistance. Nevertheless, authorities recommend replacing SHA-1 with a hash function from the SHA-2 or SHA-3 family as an additional security measure [64].

11.7.3 Hash functions in authentication-related messages

In the previous chapters, we discussed that TLS uses the following messages uniformly, that is, as a common set, for authentication, key confirmation, and handshake integrity:

• Certificate
• CertificateVerify
• Finished

Server Alice and client Bob always send these three messages as the last messages of the TLS handshake.

Recall that server Alice and client Bob compute their TLS authentication messages all uniformly by taking the following inputs:

• Their digital certificate and their private key to be used for signing
• The so-called Handshake Context that contains all handshake messages to be included in the transcript hash
• The BaseKey used to compute a MAC key

Based on the preceding inputs, the authentication messages contain the following data:

• The Certificate to be used for authentication, including any supporting certificates in the certificate chain
• The CertificateVerify signature over the value of Transcript-Hash(Handshake Context, Certificate)
• The MAC Finished, computed using the MAC key derived from from BaseKey, over the value of

Transcript-Hash(Handshake Context, Certificate, CertificateVerify)

The CertificateVerify message

Recall that Alice and Bob use the CertificateVerify message to explicitly prove that they indeed possess the private key corresponding to the public key in their certificate. In addition, CertificateVerify is used to ensure the TLS handshake’s integrity up to this point. The structure of CertificateVerify is shown in Listing 11.5.

The signature field contains the digital signature, and the algorithm field contains the signature algorithm that was used to generate the signature. Hash output of the Transcript-Hash(Handshake Context, Certificate) function is the data covered by the digital signature.

Listing 11.5: TLS 1.3 CertificateVerify message

struct {
   SignatureScheme algorithm;
   opaque signature<0..2^16-1>;
} CertificateVerify;

The Finished message

Recall that Finished is the last handshake message in the authentication block, and that this message provides authentication of the TLS handshake and authentication of the keys computed by server Alice and client Bob. The structure of the message is shown in Listing 11.6.

Listing 11.6: Structure of Finished message in TLS 1.3

struct {
   opaque verify_data[Hash.length];
} Finished;

To generate a correct Finished message, Alice and Bob use a secret key derived from the BaseKey using the HKDF-Expand-Label function:
finished_key = HKDF-Expand-Label(BaseKey, “finished”, “”, Hash.length)

Both Alice and Bob must verify the correctness of the Finished message they receive and immediately terminate the TLS session if Finished is corrupted. The verify˙data field is computed as follows:
verify_data = HMAC(finished_key, Transcript-Hash)

The Transcript-Hash is a hash value computed over c—Handshake Context—, Certificate, and CertificateVerify. The values for Certificate and CertificateVerify are included in verify˙data computation only if they were present in the TLS handshake, that is, if either server Alice or client Bob have used digital certificates to prove their identity. Now we are going to explain how Transcript-Hash is computed in detail.

11.7.4 Transcript hash

Alice and Bob use transcript hash – the hash value of the transcript of TLS handshake messages – for many cryptographic computations in TLS. The value of the transcript hash is computed by first concatenating the handshake messages and then applying a hash function to this concatenated value:

where m1,m2,…,mn are the TLS handshake messages and h is a hash function.

More precisely, the following handshake messages – but only those that were actually sent – are used in the following order as input for the transcript hash:

1. ClientHello
2. HelloRetryRequest
3. ClientHello
4. ServerHello
5. EncryptedExtensions
6. Alice’s CertificateRequest
7. Alice’s Certificate
8. Alice’s CertificateVerify
9. Alice’s Finished
10. EndOfEarlyData
11. Bob’s Certificate
12. Bob’s CertificateVerify
13. Bob’s Finished

What, in general, is the use of a transcript of a cryptographic protocol? After a protocol run is finished, the transcript allows Alice and Bob to explicitly verify that they both saw the same messages being exchanged. This, in turn, creates an additional hurdle for Mallory to mount a man-in-the-middle attack by sending Alice a message mi and Bob a different message mi′.

11.7.5 Hash functions in TLS key derivation

Recall that in order to derive TLS session keys, Alice and Bob use HKDF defined in RFC 5869 (specifically, its HKDF-Extract and HKDF-Expand functions) as well as the following two functions:
HKDF-Expand-Label(Secret, Label, Context, Length) = HKDF-Expand(Secret, HkdfLabel, Length)

and
Derive-Secret(Secret, Label, Messages) = HKDF-Expand-Label(Secret, Label, Transcript-Hash(Messages), Hash.length)

The hash function used in Transcript-Hash, HKDF-Extract, and HKDF-Expand is the hash algorithm defined in the TLS cipher suite.Hash.length is the output length of that algorithm in bytes. Finally, Messages means the concatenation of the TLS handshake messages transmitted by Alice and Bob during that specific handshake session. The HkdfLabel is a data structure shown in Listing 11.7.

Listing 11.7: The HkdfLabel data structure

struct {
   uint16 length = Length;
   opaque label<7..255> = “tls13 ” + Label;
   opaque context<0..255> = Context;
} HkdfLabel;

11.8 Summary

In this chapter, we learned how hash functions and message authentication code work, what mathematical properties they have, and how to construct them. Moreover, we covered several popular mechanisms, such as HMAC and the SHA-256, SHA-384, and SHA-512 algorithms from the SHA-2 hash algorithm family. Last but not least, we looked into the application of hash functions and message authentication code in the TLS 1.3 handshake protocol.

This chapter introduced the last building block required to understand how the TLS handshake protocol works in detail. Congratulations: you now know what Alice and Bob actually do to establish a TLS session!

In the next chapter, we will wrap up TLS 1.3 handshake. To do this, we will zoom out of the cryptographic details and give a higher-level description of TLS handshake using state machines for the TLS server and TLS client, which are specified in RFC 8446. Moreover, we will show how you can use s˙client, a TLS client program from the popular OpenSSL toolkit, to conduct your own experiments with TLS.

12.1 Key establishment in TLS 1.3

Using the TLS handshake protocol, Alice and Bob negotiate the cryptographic algorithms and key sizes. They also exchange the key shares that are required to establish the master secret. Further context-specific shared secrets and keys are then derived from this master secret according to TLS 1.3’s key derivation schedule. The secure communication channel is based on a subset of these derived secret keys.

The basic principle of TLS key establishment is shown in Figure 12.1. First, Alice and Bob negotiate cryptographic algorithms, key sizes, and exchange key shares. In the second step, Alice and Bob derive a number of context-specific TLS secrets, and in particular, a shared master secret. Each secret depends on the keying material as well as the label and the context used as inputs to generate that secret.

Finally, in the third step, Alice and Bob use the TLS secrets to derive a number of keys according to TLS 1.3’s key derivation schedule. Because the derived TLS secrets are context-specific, no further labels or additional information is needed to derive the TLS keys. However, due to context-specific secrets as input for the key derivation, the secret TLS keys are also context-specific:

Figure 12.1: A high-level view of key establishment in TLS 1.3

We will cover each of the three steps shown in Figure 12.1 in detail. As we have seen, the first step, exchange of key shares and establishment of a shared master secret over an insecure channel, can only be accomplished using a good deal of math, which is explained in Chapter 7, Public-Key Cryptography. In the present chapter, we will focus on TLS 1.3’s key derivation schedule, that is, the process of deriving further, context-specific secrets and keys from an initial secret.

12.2 TLS secrets

We saw in Chapter 3, A Secret to Share, that a good cryptographic system has multiple keys so that every key is used for a single purpose only. TLS is no exception, and in this chapter, we are going to discuss in detail what cryptographic keys client Bob and server Alice need to establish a secure TLS channel.

However, before discussing the cryptographic keys, we first need to understand what TLS secrets are and how they are derived. TLS uses a three-step approach for generation of cryptographic keys, in which the keys are generated from the secrets:

1. Alice and Bob first establish a shared master secret.
2. They derive context-specific secrets from the master secret.
3. Finally, they derive context-specific keys from these derived secrets.

Note that there is no conceptual (or cryptographic) reason to differentiate between secrets and keys. But because the TLS 1.3 specification uses this terminology and we want to provide a trustworthy guide to this specification, we felt the need to do the same differentiation here.

Table 12.1 gives an overview of secrets used in the TLS protocol and briefly explains their purpose. Don’t worry if the sheer number of TLS secrets looks overwhelming at first.

To help you, we compiled a series of graphics illustrating how the specific TLS secrets and TLS keys are interconnected. You will find the graphics at the end of the next section, Key derivation functions in TLS. In the remainder of this section, we are going to look into every TLS secret in more detail.

Secret	Purpose
Early secret	Used to generate key material if Bob and Alice use a pre-shared key (PSK) for their TLS handshake.
Binder	Establishes a binding between the PSK and current TLS handshake.
Early traffic secret	Used by Bob to encrypt early handshake traffic if the PSK is used for the TLS handshake.
Exporter secrets	Secrets that can be used outside of the TLS protocol to derive additional secret keys for higher-layer protocols or applications running on top of TLS.
Derived secrets	Intermediate secrets used as salt arguments for deriving TLS secrets.
Handshake secret	This secret is the result of the handshake. It is either derived from the early secret in case a PSK is in place or from a Diffie-Hellman key exchange between Alice and Bob. It is used as input to generate the following two TLS secrets: Bob’s handshake traffic secret and Alice’s handshake traffic secret.
Handshake traffic secrets	Used to generate TLS handshake traffic keys, one for Bob and one for Alice.
Master secret	Used as input to generate the following two TLS secrets: Bob’s application traffic secret and Alice’s application traffic secret.
Application traffic secrets	Used to generate TLS application traffic keys. Like with handshake traffic keys, one key is for Bob and one is for Alice.
Resumption master secret	Used for session resumption.

 Table 12.1: Overview of secrets used in TLS (see also [53])

12.2.1 Early secret

TLS 1.3 offers the option for Alice and Bob to use a pre-shared secret key PSK. This is a key Alice and Bob have previously agreed on independent of TLS. If Alice and Bob use a PSK for their TLS handshake, they derive the early secret from PSK and use it as input keying material (IKM) to generate binder˙key, client˙early˙traffic˙secret, and early˙exporter˙master˙secret, which will be explained later in this chapter.

12.2.2 Binder key

The binder key is used to establish a binding between Alice’s and Bob’s pre-shared secret key and their current TLS handshake as well as between the current TLS handshake and the previous TLS handshake where that PSK was generated. In other words, Bob uses the binder to prove to Alice that he indeed knows the PSK associated with the identity known to Alice.

Alice uses the PSK binder to verify that Bob actually knows the correct PSK before actually executing a PSK-based TLS handshake. If the verification fails or Bob does not present the binder to Alice, she immediately aborts the TLS handshake. This ensures that Alice does not execute a PSK-based handshake without verifying that Bob actually knows the PSK.

By binding a previous TLS session where the binder key was generated to the current TLS handshake, this mechanism also allows Alice to implicitly verify that Bob did not suffer a man-in-the-middle attack. If Mallory managed to perform a successful man-in-the-middle attack, Alice and Bob would have a different PSK and this would prevent a subsequent TLS session resumption.

12.2.3 Bob’s client early traffic secret.

If a PSK is used for the TLS handshake, client˙early˙traffic˙secret can be used to generate a key that allows Bob to encrypt early application data in the first ClientHello message of the TLS handshake. This key is only used by Bob.

12.2.4 Exporter secrets

Exporter secrets are secrets used to derive additional secret keys for use outside of the TLS protocol. Some higher-level protocols use TLS to establish a shared secret key and afterward use TLS keying material for other protocol-specific purposes. This, in turn, requires exporting keying material to higher-layer protocols or applications as well as agreeing on the context in which that keying material will be used.

For example, the DTLS-SRTP protocol first uses Datagram-TLS (DTLS) to exchange secret keys and selects the Secure Real-Time Transport Protocol (SRTP) protection suite. Subsequently, it uses DTLS master˙secret to derive SRTP keys.

To enable this, TLS offers a mechanism called Key Material Exporter, details of which are defined in RFC 5705 [145]. The exported values are referred to as Exported Keying Material (EKM). In TLS, early˙exporter˙master˙secret and exporter˙master˙secret are examples of EKM generated at different stages of the TLS handshake.

TLS exporters have the following cryptographic properties:

• They allow Bob and Alice to export the same EKM value
• For attacker Eve who does not know the master˙secret, EKM is indistinguishable from a random number
• Bob and Alice can export multiple EKM values from a single TLS connection
• Even if Eve learns one EKM value, she learns nothing about other EKM values or the master˙secret

12.2.5 Derived secrets

These are intermediate secrets that are used as salt arguments for the HKDF-Extract function (which we will shortly discuss in detail). The HKDF-Extract function, in turn, generates the Handshake Secret and the Master Secret.

12.2.6 Handshake secret

This secret is the final result of the handshake. It is either derived from the Early Secret if a PSK is in place or from the secret Alice and Bob have exchanged during a Diffie-Hellman. The Handshake Secret is used to derive the client˙handshake˙traffic˙secret for Bob and the server˙handshake˙traffic˙secret for Alice.

12.2.7 Handshake traffic secrets

Bob subsequently uses the client˙handshake˙traffic˙secret secret and Alice uses the server˙handshake˙traffic˙secret secret to generate secret keys for their handshake traffic encryption.

12.2.8 Master secret

The Master Secret is used to derive the client˙application˙traffic˙secret0 for Bob and the server˙application˙traffic˙secret0 for Alice. These secrets can be updated later during a TLS session, hence their index 0.

12.2.9 Application traffic secrets

The client˙application˙traffic˙secret0 is used by Bob and the server˙application˙traffic˙secret0 is used by Alice to generate corresponding secret keys for encryption of the application data. These keys allow Alice and Bob to establish a secure channel for the bulk application data. TLS also has an optional mechanism to update these secrets and, in turn, these keys during a TLS session.

12.2.10 Resumption master secret

This secret is used to derive the pre-shared secret key for TLS session resumption. After a successful handshake, Alice can send Bob the identity of a PSK derived during that handshake. Bob can then use this PSK identity in subsequent TLS handshakes with Alice in order to signal his desire to use the associated PSK.

We now turn to the question of how the secrets are derived from the exchanged keying material.

12.3 KDFs in TLS

TLS uses four different functions to derive secrets: HKDF-Extract, HKDF-Expand, HKDF-Expand-Label, and Derive-Secret. All these functions are based on the Hashed Message Authentication Code (HMAC)-based Extract-and-Expand Key Derivation Function (HKDF) defined in RFC 5869 [104].

We will have much more to say on hash functions, message authentication codes, and key derivation function in Chapter 11, Hash Functions and Message Authentication Codes. For now, it is sufficient to treat HKDF as an abstract function, as shown in Figure 12.2. It takes keying material as input and returns one or more secret keys as output:

Figure 12.2: High-level view of the HKDF function

HKDF follows an extract-then-expand approach consisting of two logical stages. The rationale for this two-step approach is explained nicely in the introduction of [104]: ”In many applications, the input keying material is not necessarily distributed uniformly, and the attacker may have some partial knowledge about it (for example, a Diffie-Hellman value computed by a key exchange protocol) or even partial control of it (as in some entropy-gathering applications). Thus, the goal of the extract-stage is to concentrate the possibly dispersed entropy of the input keying material into a short, but cryptographically strong, pseudorandom key. In some applications, the input may already be a good pseudorandom key; in these cases, the extract-stage is not necessary, and the ”expand” part can be used alone. The second stage expands the pseudorandom key to the desired length; the number and lengths of the output keys depend on the specific cryptographic algorithms for which the keys are needed.”

Now, let’s take a look at the extract-and-expand-functions in HKDFs.

12.3.1 HKDF-Extract

HKDF-Extract, or HE for short, implements the first stage of the HKDF, which takes the keying material as input and extracts a fixed-length pseudorandom key K from it. In particular, it is involved in the derivation of the handshake secret SH and the master secret SM (see Figure 12.9 and Figure 12.11, respectively).

HKDF-Extract is illustrated in Figure 12.3. It takes two inputs: a salt and an input keying material (IKM). The salt is a non-secret random value. If no salt is provided, HKDF-Extract takes a string of zeros of the length equal to that of the hash function output. HKDF-Extract outputs a pseudorandom key (PRK). The PRK is calculated as PRK = HMAC-Hash(salt, IKM). Since HKDF-Extract is based on the HMAC construction, which is in turn a construction template that can use different hash functions [103], HKDF-Extract can also use different cryptographic hash functions.

Figure 12.3: HKDF-Extract function used for TLS key derivation

A new TLS secret is derived using HKDF-Extract with the current TLS secret state as salt and the PSK – established out of band or derived from the resumption˙master˙secret instance of a previous TLS session – or the DHE or ECDHE based shared secret that Alice and Bob have established during the current TLS handshake as IKM.

12.3.2 HKDF-Expand

The second stage of the HKDF function expands a PRK to a pseudorandom bit string of the desired length, which can then be used to derive secret keys. HKDF-Expand is illustrated in Figure 12.4.

HKDF-Expand takes three inputs: a pseudorandom key PRK (which must have at least the length of the output of the hash function used), an optional context and application-specific information info, and the desired length in bytes of the output keying material L.

The output of HKDF-Expand is an L-byte long Output Keying Material (OKM). The OKM is calculated by first calculating the following N values, where N is the result of the ceiling function applied to (L∕HashLen):

T(0) = empty string(zero length)

T(1) = HMAC-Hash(PRK,T(0)|info|0x01)

T(2) = HMAC-Hash(PRK,T(1)|info|0x02)

 …

T(N) = HMAC-Hash(PRK,T(N − 1)|info|N)

where | denotes the bit-wise concatenation. The HMAC construction for key-dependent hash values is explained in Section 11.5, Message authentication codes. After that, the OKM is built by taking the first L octets of T = T(1)|T(2)|…|T(N).

Figure 12.4: The HKDF-Expand function HP

After each invocation of the HKDF-Extract function, the HKDF-Expand function is invoked one or more times.