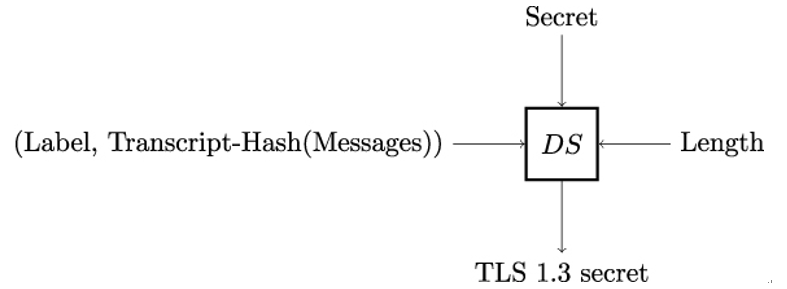
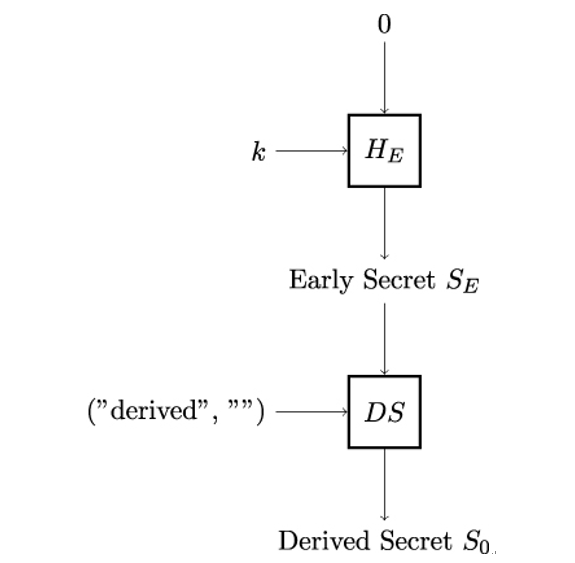
11.7 Hash functions in TLS 1.3

We’ll now take a look at how hash functions are negotiated within the TLS handshake and how they are subsequently used in the handshake.

11.7.1 Hash functions in ClientHello

Recall that Alice and Rob use the TLS handshake protocol to negotiate the security parameters for their connection. They do it using TLS handshake messages shown in Listing 11.3. Once assembled by the TLS endpoint – that is, server Alice or client Bob – these messages are passed to the TLS record layer where they are embedded into one or more TLSPlaintext or TLSCiphertext data structures. The data structures are then transmitted according to the current state of the TLS connection.

Listing 11.3: TLS 1.3 handshake messages

enum {
   client_hello(1),
   server_hello(2),
   new_session_ticket(4),
   end_of_early_data(5),
   encrypted_extensions(8),
   certificate(11),
   certificate_request(13),
   certificate_verify(15),
   finished(20),
   key_update(24),
   message_hash(254),
   (255)
} HandshakeType;

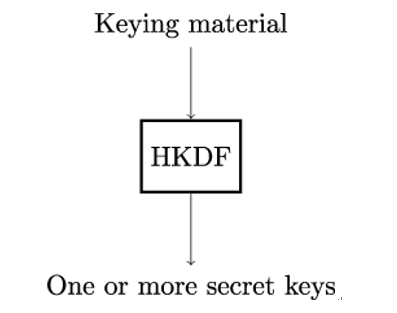
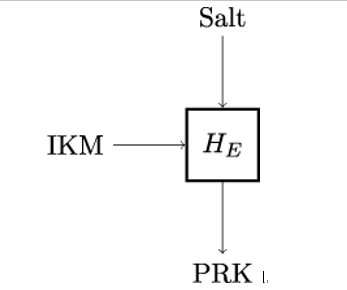
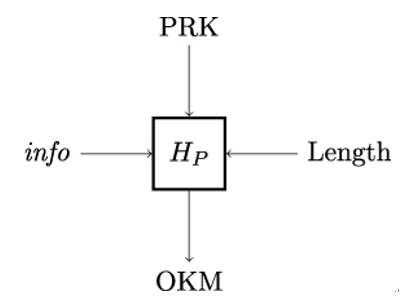
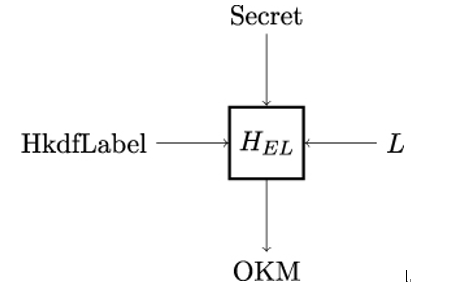
One of the most important TLS handshake messages is ClientHello since this message starts a TLS session between client Bob and server Alice. The structure of the ClientHello message is shown in Listing 11.4. The cipher˙suites field in ClientHello carries a list of symmetric key algorithms supported by client Bob, specifically the encryption algorithm protecting the TLS record layer and the hash function used with the HMAC-based key derivation function HKDF.

Listing 11.4: TLS 1.3 ClientHello message

struct {
   ProtocolVersion legacy_version = 0x0303;    /* TLS v1.2 */
   Random random;
   opaque legacy_session_id<0..32>;
   CipherSuite cipher_suites<2..2^16-2>;
   opaque legacy_compression_methods<1..2^8-1>;
   Extension extensions<8..2^16-1>;
} ClientHello;

11.7.2 Hash Functions in TLS 1.3 signature schemes

Recall that server Alice and client Bob also agree upon the signature scheme they will use during the TLS handshake. The SignatureScheme field indicates the signature algorithm with the corresponding hash function. The following code shows digital signature schemes supported in TLS 1.3:

enum {
    /* RSASSA-PKCS1-v1_5 algorithms */
    rsa_pkcs1_sha256(0x0401),
    rsa_pkcs1_sha384(0x0501),
    rsa_pkcs1_sha512(0x0601),
    /* ECDSA algorithms */
    ecdsa_secp256r1_sha256(0x0403),
    ecdsa_secp384r1_sha384(0x0503),
    ecdsa_secp521r1_sha512(0x0603),
    /* RSASSA-PSS algorithms with public key OID rsaEncryption */
    rsa_pss_rsae_sha256(0x0804),
    rsa_pss_rsae_sha384(0x0805),
    rsa_pss_rsae_sha512(0x0806),
    /* EdDSA algorithms */
    ed25519(0x0807),
    ed448(0x0808),
    /* RSASSA-PSS algorithms with public key OID RSASSA-PSS */
    rsa_pss_pss_sha256(0x0809),
    rsa_pss_pss_sha384(0x080a),
    rsa_pss_pss_sha512(0x080b),
    — snip —
} SignatureScheme;

We’ll now discuss the SHA family of hash functions in detail.

SHA-1

SHA-1 is a hash algorithm that was in use from 1995 as part of the FIPS standard 180-1, but has been deprecated by NIST, BSI, and other agencies due to severe security issues with regard to its collision resistance. In 2005, a team of Chinese researchers published the first cryptanalytic attacks against the SHA-1 algorithm. These theoretical attacks allowed the researchers to find collisions with much less work than with a brute-force attack. Following further improvements in these attacks, NIST deprecated SHA-1 in 2011 and disallowed using it for digital signatures in 2013.

In 2017, a team of researchers from the CWI Institute in Amsterdam and Google published Shattered, the first practical attack on SHA-1, by crafting two different PDF files having an identical SHA-1 signature. You can test the attack yourself at https://shattered.io/.

Finally, in 2020, two French researchers published the first practical chosen-prefix collision attack against SHA-1. Using the attack, Mallory can build colliding messages with two arbitrary prefixes. This is much more threatening for cryptographic protocols, and the researchers have demonstrated their work by mounting a PGP/GnuPG impersonation attack. Moreover, the cost of computing such chosen-prefix collisions has been significantly reduced over time and is now considered to be within the reach of attackers with computing resources similar to those of academic researchers [64].

While SHA-1 must not be used as a secure cryptographic hash function, it may still be used in other cryptographic applications [64]. As an example, based on what is known today, SHA-1 can be used for HMAC because the HMAC construction does not require collision resistance. Nevertheless, authorities recommend replacing SHA-1 with a hash function from the SHA-2 or SHA-3 family as an additional security measure [64].

11.7.3 Hash functions in authentication-related messages

In the previous chapters, we discussed that TLS uses the following messages uniformly, that is, as a common set, for authentication, key confirmation, and handshake integrity:

• Certificate
• CertificateVerify
• Finished

Server Alice and client Bob always send these three messages as the last messages of the TLS handshake.

Recall that server Alice and client Bob compute their TLS authentication messages all uniformly by taking the following inputs:

• Their digital certificate and their private key to be used for signing
• The so-called Handshake Context that contains all handshake messages to be included in the transcript hash
• The BaseKey used to compute a MAC key

Based on the preceding inputs, the authentication messages contain the following data:

• The Certificate to be used for authentication, including any supporting certificates in the certificate chain
• The CertificateVerify signature over the value of Transcript-Hash(Handshake Context, Certificate)
• The MAC Finished, computed using the MAC key derived from from BaseKey, over the value of

Transcript-Hash(Handshake Context, Certificate, CertificateVerify)

The CertificateVerify message

Recall that Alice and Bob use the CertificateVerify message to explicitly prove that they indeed possess the private key corresponding to the public key in their certificate. In addition, CertificateVerify is used to ensure the TLS handshake’s integrity up to this point. The structure of CertificateVerify is shown in Listing 11.5.

The signature field contains the digital signature, and the algorithm field contains the signature algorithm that was used to generate the signature. Hash output of the Transcript-Hash(Handshake Context, Certificate) function is the data covered by the digital signature.

Listing 11.5: TLS 1.3 CertificateVerify message

struct {
   SignatureScheme algorithm;
   opaque signature<0..2^16-1>;
} CertificateVerify;

The Finished message

Recall that Finished is the last handshake message in the authentication block, and that this message provides authentication of the TLS handshake and authentication of the keys computed by server Alice and client Bob. The structure of the message is shown in Listing 11.6.

Listing 11.6: Structure of Finished message in TLS 1.3

struct {
   opaque verify_data[Hash.length];
} Finished;

To generate a correct Finished message, Alice and Bob use a secret key derived from the BaseKey using the HKDF-Expand-Label function:
finished_key = HKDF-Expand-Label(BaseKey, “finished”, “”, Hash.length)

Both Alice and Bob must verify the correctness of the Finished message they receive and immediately terminate the TLS session if Finished is corrupted. The verify˙data field is computed as follows:
verify_data = HMAC(finished_key, Transcript-Hash)

The Transcript-Hash is a hash value computed over c—Handshake Context—, Certificate, and CertificateVerify. The values for Certificate and CertificateVerify are included in verify˙data computation only if they were present in the TLS handshake, that is, if either server Alice or client Bob have used digital certificates to prove their identity. Now we are going to explain how Transcript-Hash is computed in detail.

12.1 Key establishment in TLS 1.3

Using the TLS handshake protocol, Alice and Bob negotiate the cryptographic algorithms and key sizes. They also exchange the key shares that are required to establish the master secret. Further context-specific shared secrets and keys are then derived from this master secret according to TLS 1.3’s key derivation schedule. The secure communication channel is based on a subset of these derived secret keys.

The basic principle of TLS key establishment is shown in Figure 12.1. First, Alice and Bob negotiate cryptographic algorithms, key sizes, and exchange key shares. In the second step, Alice and Bob derive a number of context-specific TLS secrets, and in particular, a shared master secret. Each secret depends on the keying material as well as the label and the context used as inputs to generate that secret.

Finally, in the third step, Alice and Bob use the TLS secrets to derive a number of keys according to TLS 1.3’s key derivation schedule. Because the derived TLS secrets are context-specific, no further labels or additional information is needed to derive the TLS keys. However, due to context-specific secrets as input for the key derivation, the secret TLS keys are also context-specific:

Figure 12.1: A high-level view of key establishment in TLS 1.3

We will cover each of the three steps shown in Figure 12.1 in detail. As we have seen, the first step, exchange of key shares and establishment of a shared master secret over an insecure channel, can only be accomplished using a good deal of math, which is explained in Chapter 7, Public-Key Cryptography. In the present chapter, we will focus on TLS 1.3’s key derivation schedule, that is, the process of deriving further, context-specific secrets and keys from an initial secret.

12.2 TLS secrets

We saw in Chapter 3, A Secret to Share, that a good cryptographic system has multiple keys so that every key is used for a single purpose only. TLS is no exception, and in this chapter, we are going to discuss in detail what cryptographic keys client Bob and server Alice need to establish a secure TLS channel.

However, before discussing the cryptographic keys, we first need to understand what TLS secrets are and how they are derived. TLS uses a three-step approach for generation of cryptographic keys, in which the keys are generated from the secrets:

1. Alice and Bob first establish a shared master secret.
2. They derive context-specific secrets from the master secret.
3. Finally, they derive context-specific keys from these derived secrets.

Note that there is no conceptual (or cryptographic) reason to differentiate between secrets and keys. But because the TLS 1.3 specification uses this terminology and we want to provide a trustworthy guide to this specification, we felt the need to do the same differentiation here.

Table 12.1 gives an overview of secrets used in the TLS protocol and briefly explains their purpose. Don’t worry if the sheer number of TLS secrets looks overwhelming at first.

To help you, we compiled a series of graphics illustrating how the specific TLS secrets and TLS keys are interconnected. You will find the graphics at the end of the next section, Key derivation functions in TLS. In the remainder of this section, we are going to look into every TLS secret in more detail.

Secret	Purpose
Early secret	Used to generate key material if Bob and Alice use a pre-shared key (PSK) for their TLS handshake.
Binder	Establishes a binding between the PSK and current TLS handshake.
Early traffic secret	Used by Bob to encrypt early handshake traffic if the PSK is used for the TLS handshake.
Exporter secrets	Secrets that can be used outside of the TLS protocol to derive additional secret keys for higher-layer protocols or applications running on top of TLS.
Derived secrets	Intermediate secrets used as salt arguments for deriving TLS secrets.
Handshake secret	This secret is the result of the handshake. It is either derived from the early secret in case a PSK is in place or from a Diffie-Hellman key exchange between Alice and Bob. It is used as input to generate the following two TLS secrets: Bob’s handshake traffic secret and Alice’s handshake traffic secret.
Handshake traffic secrets	Used to generate TLS handshake traffic keys, one for Bob and one for Alice.
Master secret	Used as input to generate the following two TLS secrets: Bob’s application traffic secret and Alice’s application traffic secret.
Application traffic secrets	Used to generate TLS application traffic keys. Like with handshake traffic keys, one key is for Bob and one is for Alice.
Resumption master secret	Used for session resumption.

 Table 12.1: Overview of secrets used in TLS (see also [53])

12.2.1 Early secret

TLS 1.3 offers the option for Alice and Bob to use a pre-shared secret key PSK. This is a key Alice and Bob have previously agreed on independent of TLS. If Alice and Bob use a PSK for their TLS handshake, they derive the early secret from PSK and use it as input keying material (IKM) to generate binder˙key, client˙early˙traffic˙secret, and early˙exporter˙master˙secret, which will be explained later in this chapter.

12.2.2 Binder key

The binder key is used to establish a binding between Alice’s and Bob’s pre-shared secret key and their current TLS handshake as well as between the current TLS handshake and the previous TLS handshake where that PSK was generated. In other words, Bob uses the binder to prove to Alice that he indeed knows the PSK associated with the identity known to Alice.

Alice uses the PSK binder to verify that Bob actually knows the correct PSK before actually executing a PSK-based TLS handshake. If the verification fails or Bob does not present the binder to Alice, she immediately aborts the TLS handshake. This ensures that Alice does not execute a PSK-based handshake without verifying that Bob actually knows the PSK.

By binding a previous TLS session where the binder key was generated to the current TLS handshake, this mechanism also allows Alice to implicitly verify that Bob did not suffer a man-in-the-middle attack. If Mallory managed to perform a successful man-in-the-middle attack, Alice and Bob would have a different PSK and this would prevent a subsequent TLS session resumption.

12.2.3 Bob’s client early traffic secret.

If a PSK is used for the TLS handshake, client˙early˙traffic˙secret can be used to generate a key that allows Bob to encrypt early application data in the first ClientHello message of the TLS handshake. This key is only used by Bob.

12.2.4 Exporter secrets

Exporter secrets are secrets used to derive additional secret keys for use outside of the TLS protocol. Some higher-level protocols use TLS to establish a shared secret key and afterward use TLS keying material for other protocol-specific purposes. This, in turn, requires exporting keying material to higher-layer protocols or applications as well as agreeing on the context in which that keying material will be used.

For example, the DTLS-SRTP protocol first uses Datagram-TLS (DTLS) to exchange secret keys and selects the Secure Real-Time Transport Protocol (SRTP) protection suite. Subsequently, it uses DTLS master˙secret to derive SRTP keys.

To enable this, TLS offers a mechanism called Key Material Exporter, details of which are defined in RFC 5705 [145]. The exported values are referred to as Exported Keying Material (EKM). In TLS, early˙exporter˙master˙secret and exporter˙master˙secret are examples of EKM generated at different stages of the TLS handshake.

TLS exporters have the following cryptographic properties:

• They allow Bob and Alice to export the same EKM value
• For attacker Eve who does not know the master˙secret, EKM is indistinguishable from a random number
• Bob and Alice can export multiple EKM values from a single TLS connection
• Even if Eve learns one EKM value, she learns nothing about other EKM values or the master˙secret

12.2.5 Derived secrets

These are intermediate secrets that are used as salt arguments for the HKDF-Extract function (which we will shortly discuss in detail). The HKDF-Extract function, in turn, generates the Handshake Secret and the Master Secret.

12.2.6 Handshake secret

This secret is the final result of the handshake. It is either derived from the Early Secret if a PSK is in place or from the secret Alice and Bob have exchanged during a Diffie-Hellman. The Handshake Secret is used to derive the client˙handshake˙traffic˙secret for Bob and the server˙handshake˙traffic˙secret for Alice.

12.2.7 Handshake traffic secrets

Bob subsequently uses the client˙handshake˙traffic˙secret secret and Alice uses the server˙handshake˙traffic˙secret secret to generate secret keys for their handshake traffic encryption.

12.2.8 Master secret

The Master Secret is used to derive the client˙application˙traffic˙secret0 for Bob and the server˙application˙traffic˙secret0 for Alice. These secrets can be updated later during a TLS session, hence their index 0.

12.2.9 Application traffic secrets

The client˙application˙traffic˙secret0 is used by Bob and the server˙application˙traffic˙secret0 is used by Alice to generate corresponding secret keys for encryption of the application data. These keys allow Alice and Bob to establish a secure channel for the bulk application data. TLS also has an optional mechanism to update these secrets and, in turn, these keys during a TLS session.

12.2.10 Resumption master secret

This secret is used to derive the pre-shared secret key for TLS session resumption. After a successful handshake, Alice can send Bob the identity of a PSK derived during that handshake. Bob can then use this PSK identity in subsequent TLS handshakes with Alice in order to signal his desire to use the associated PSK.

We now turn to the question of how the secrets are derived from the exchanged keying material.

12.3 KDFs in TLS

TLS uses four different functions to derive secrets: HKDF-Extract, HKDF-Expand, HKDF-Expand-Label, and Derive-Secret. All these functions are based on the Hashed Message Authentication Code (HMAC)-based Extract-and-Expand Key Derivation Function (HKDF) defined in RFC 5869 [104].

We will have much more to say on hash functions, message authentication codes, and key derivation function in Chapter 11, Hash Functions and Message Authentication Codes. For now, it is sufficient to treat HKDF as an abstract function, as shown in Figure 12.2. It takes keying material as input and returns one or more secret keys as output:

Figure 12.2: High-level view of the HKDF function

HKDF follows an extract-then-expand approach consisting of two logical stages. The rationale for this two-step approach is explained nicely in the introduction of [104]: ”In many applications, the input keying material is not necessarily distributed uniformly, and the attacker may have some partial knowledge about it (for example, a Diffie-Hellman value computed by a key exchange protocol) or even partial control of it (as in some entropy-gathering applications). Thus, the goal of the extract-stage is to concentrate the possibly dispersed entropy of the input keying material into a short, but cryptographically strong, pseudorandom key. In some applications, the input may already be a good pseudorandom key; in these cases, the extract-stage is not necessary, and the ”expand” part can be used alone. The second stage expands the pseudorandom key to the desired length; the number and lengths of the output keys depend on the specific cryptographic algorithms for which the keys are needed.”

Now, let’s take a look at the extract-and-expand-functions in HKDFs.

12.3.1 HKDF-Extract

HKDF-Extract, or HE for short, implements the first stage of the HKDF, which takes the keying material as input and extracts a fixed-length pseudorandom key K from it. In particular, it is involved in the derivation of the handshake secret SH and the master secret SM (see Figure 12.9 and Figure 12.11, respectively).

HKDF-Extract is illustrated in Figure 12.3. It takes two inputs: a salt and an input keying material (IKM). The salt is a non-secret random value. If no salt is provided, HKDF-Extract takes a string of zeros of the length equal to that of the hash function output. HKDF-Extract outputs a pseudorandom key (PRK). The PRK is calculated as PRK = HMAC-Hash(salt, IKM). Since HKDF-Extract is based on the HMAC construction, which is in turn a construction template that can use different hash functions [103], HKDF-Extract can also use different cryptographic hash functions.

Figure 12.3: HKDF-Extract function used for TLS key derivation

A new TLS secret is derived using HKDF-Extract with the current TLS secret state as salt and the PSK – established out of band or derived from the resumption˙master˙secret instance of a previous TLS session – or the DHE or ECDHE based shared secret that Alice and Bob have established during the current TLS handshake as IKM.

12.3.2 HKDF-Expand

The second stage of the HKDF function expands a PRK to a pseudorandom bit string of the desired length, which can then be used to derive secret keys. HKDF-Expand is illustrated in Figure 12.4.

HKDF-Expand takes three inputs: a pseudorandom key PRK (which must have at least the length of the output of the hash function used), an optional context and application-specific information info, and the desired length in bytes of the output keying material L.

The output of HKDF-Expand is an L-byte long Output Keying Material (OKM). The OKM is calculated by first calculating the following N values, where N is the result of the ceiling function applied to (L∕HashLen):

T(0) = empty string(zero length)

T(1) = HMAC-Hash(PRK,T(0)|info|0x01)

T(2) = HMAC-Hash(PRK,T(1)|info|0x02)

 …

T(N) = HMAC-Hash(PRK,T(N − 1)|info|N)

where | denotes the bit-wise concatenation. The HMAC construction for key-dependent hash values is explained in Section 11.5, Message authentication codes. After that, the OKM is built by taking the first L octets of T = T(1)|T(2)|…|T(N).

Figure 12.4: The HKDF-Expand function HP

After each invocation of the HKDF-Extract function, the HKDF-Expand function is invoked one or more times.

12.3.3 HKDF-Expand-Label

HKDF-Expand-Label (or HEL for short) is a pseudorandom function as shown in Figure 12.5. Recall this means that it can be efficiently computed for any given input, but it cannot be efficiently distinguished from a uniformly random function [37].

HKDF-Expand-Label takes a secret, the desired length of the output L, and an HKDF-Label as input, and expands them to OKM.

Figure 12.5: The HKDF-Expand-Label function HEL

The HkdfLabel data structure is defined as in Listing 12.1. It essentially consists of a label and a context. All labels used in TLS 1.3 are strings. The context might have zero length.

Listing 12.1: HkdfLabel data structure

struct {
   uint16 length = Length;
   opaque label<7..255> = “tls13 ” + Label;
   opaque context<0..255> = Context;
} HkdfLabel;

HKDF-Expand-Label illustrates a cryptographic good practice where keying material and, in turn, keys are derived for a specific purpose using a label and a context as inputs to the KDF.

12.3.4 Derive-Secret

Finally, the TLS 1.3 Derive-Secret function DS is defined as shown in Figure 12.6. It takes a secret, a label, and TLS messages as input, and outputs one of the TLS secrets listed in Table 12.1. In the subsequent step, these secrets will be used to derive the TLS keys.

As a result, multiple calls to Derive-Secret can be used to derive keying material for different secret keys even with the same secret as input as long as different messages are used to compute the transcript hash.

Figure 12.6: The Derive-Secret function DS

Derive-Secret implements a clever way to bind the keying material to previous messages exchanged during a specific execution of a cryptographic protocol. This is desirable from a cryptography perspective because it causes Alice and Bob to derive completely different secret keys and, as a result, leads to a failure of the cryptographic protocol since Alice cannot understand what Bob encrypted or authenticated, and vice versa.

This approach implements an implicit protection against man-in-the-middle attacks. Even if Mallory manages to intercept and manipulate messages exchanged by Alice and Bob, she cannot trick them into deriving an identical secret key because Alice’s message transcript will be different from Bob’s message transcript.

As illustrated in Figure 12.7, Alice and Bob start by deriving the Early Secret SE and an intermediate secret S0 (which will be used for further computations). Eventually, Alice and Bob will establish a secure TLS channel by deriving the shared cryptographic keys from these secrets.

Figure 12.7: Derivation of the TLS early secret and first derived secret S0

If a specific TLS secret is not available, a zero value – a string of 0-valued bytes – is taken as input. As an example, if the pre-shared key PSK is not used, the early secret will be computed as follows:
Early_Secret = HKDF-Extract(0, 0)