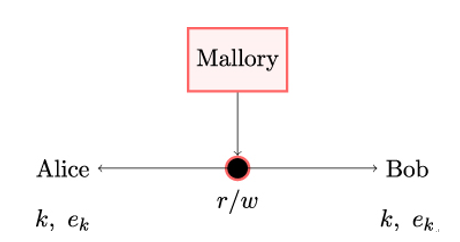
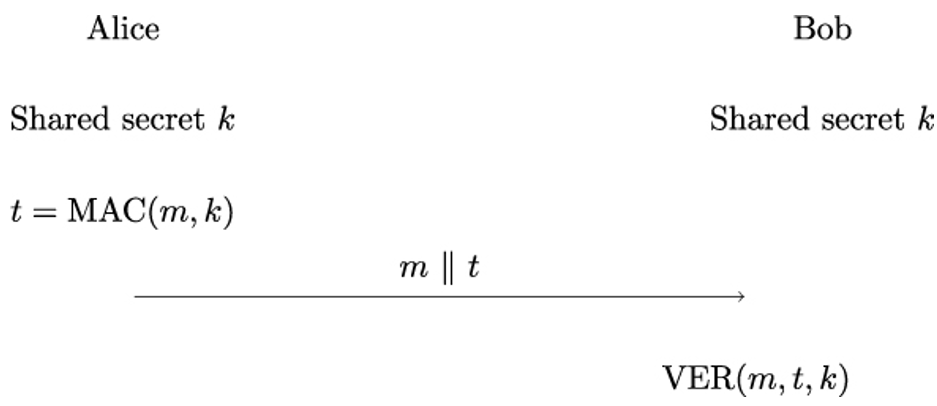
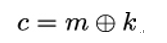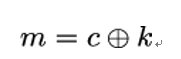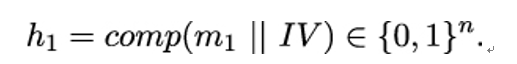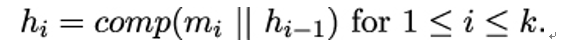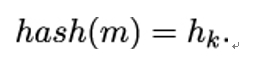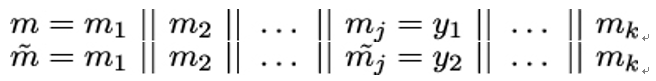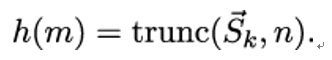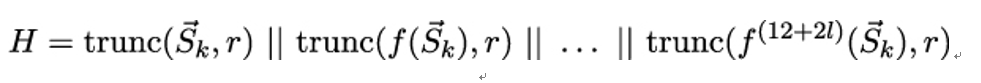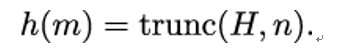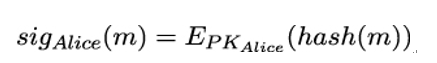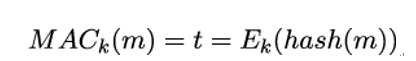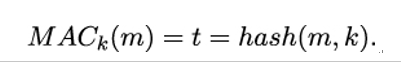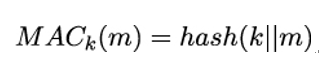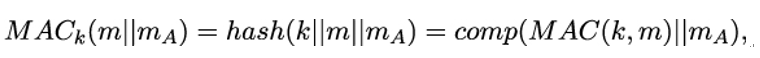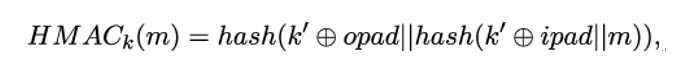10.2.6 X.509 trust model

Generally speaking, there are three steps in verifying a certificate:

• Verify that the certificate has not been revoked
• Verify that the certificate is valid (for instance, verify the certificate’s extensions and its validity period)
• Verify the signature of the CA over the certificate

As discussed earlier, the first step consists of either consulting a CRL or an OCSP server. But to verify the signature over a certificate (or a CRL or an OCSP response), we need an authentic copy of the CA’s public key – in other words, we need another certificate, in which the original CA is the subject. In X.509, these CA certificates are issued by a higher-order CA, which in turn has a certificate from an even higher-order CA, so that a hierarchical tree structure emerges with a Root CA at the top, which certifies itself (see Figure 10.4).

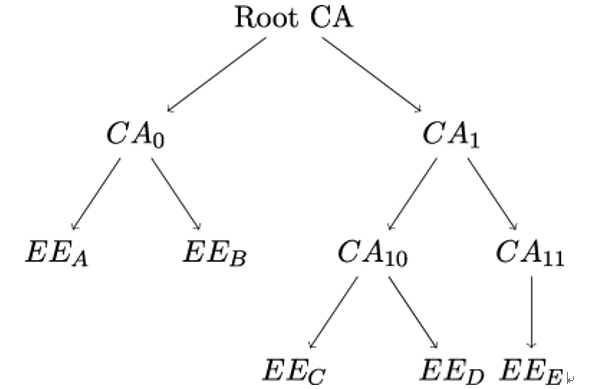
Figure 10.4: X.509 hierarchical trust model. An arrow from X to Y means that X certifies Y . EE stands for End Entity

The Path Length Constraint within the Basic Constraints extension field limits the number of CA certificates that may follow a CA certificate down the tree until the EE certificate under consideration is reached. For CA0 in Figure 10.4, for example, the path length constraint could be set to 0, whereas for CA1, the path length constraint should be at least 1, lest verification of the end entity certificates for C,D, and E fails.

In practice, a CA is rarely certified by another, independent CA. Rather, there are instances within the same company that act as root CAs for their own intermediate CA instances. From a security perspective, this is equivalent to a CA self-signing its own public key. This means that, in most cases, the relying parties cannot transfer the question of whether to trust a particular CA to some independent higher-order instance, but must base their trust decisions entirely on the publicly available information about a CA, for example, the CPS. Although modern browsers contain lists of trusted CAs, it is not entirely clear how these lists come about, and they should be no substitute for making your own decisions.

10.5 Digital certificates in TLS

Now we will take a look at how certificates are handled within the TLS handshake protocol. We start by discussing TLS extensions, which provide a way to transport data in request-response type message exchanges within TLS. The rest of the section is broadly organized according to the TLS extensions dealing with digital certificates and certification authorities.

10.5.1 TLS extensions

Some TLS messages include the tag-value data structure shown in Listing  10.1 and referred to as an extension. The extension˙type field specifies the type of the extension, and the extension˙data field stores the corresponding data.

Listing 10.1: Data structure of a TLS extension

struct {
   ExtensionType extension_type;
   opaque extension_data<0..2^16-1>;
} Extension;

Typically, TLS extensions are used in a request-response message exchange: client Bob sends an extension request in his ClientHello message, and server Alice replies with an extension response in her ServerHello, EncryptedExtensions, HelloRetryRequest, or Certificate message.

If server Alice sends an extension request in her CertificateRequest message, client Bob may respond with a Certificate message.

10.5.2 Encrypted extensions

In TLS 1.3 handshake, server Alice sends the EncryptedExtensions message immediately after her ServerHello message. At this point, Alice and Bob have agreed on a secret and have subsequently derived a shared key. The EncryptedExtensions message is the first encrypted message in the TLS handshake. The data structure is shown in Listing 10.2.

Listing 10.2: TLS encrypted extension data structure

struct {
   Extension extensions<0..2^16-1>;
} EncryptedExtensions;

10.5.3 Certificate request

If server Alice authenticates herself to client Bob using a certificate, she may request Bob to present his certificate too. This request must be sent directly after EncryptedExtensions and the corresponding message has the structure shown in Listing 10.3.

Listing 10.3: Server Alice’s certificate request

struct {
   opaque certificate_request_context<0..2^8-1>;
   Extension extensions<2..2^16-1>;
} CertificateRequest;

The preceding is a good illustration of how optional interaction between communicating parties can be added to a cryptographic protocol to further improve security, if this is desired by Alice and Bob. Requiring client Bob to also prove his identity, in this case using a digital certificate, results in a mutual authentication where both client Bob as well as server Alice can verify each other’s identity and so know whom they are communicating with.

10.5.7 The CertificateVerify message

The CertificateVerify message provides explicit proof that the sender—either client Bob or server Alice—indeed has the private key corresponding to its certificate. Moreover, the CertificateVerify message allows you to verify the integrity of the TLS handshake up to this point. Listing 10.6 shows the structure of the CertificateVerify message:

Listing 10.6: Structure of the CertificateVerify message

struct {
   SignatureScheme algorithm;
   opaque signature<0..2^16-1>;
} CertificateVerify;

The algorithm field in Listing 10.6 holds the signature algorithm used to generate the signature. The content covered by the signature includes the TLS handshake context and the certificate.

The signature is computed over a concatenation of the following data:

• A string consisting of 64 bytes having a value of 32
• The TLS 1.3, server CertificateVerify string for server Alice’s signature and the TLS 1.3, client CertificateVerify string for client Bob’s signature
• A single byte having value 0 that acts as a separator
• The content to be signed

The context string secures TLS against cross-protocol attacks by providing a way to differentiate between the signatures generated in different contexts.

Server Alice sends the CertificateVerify message when she authenticates herself to client Bob using a certificate. Client Bob sends CertificateVerify whenever he authenticates himself using a certificate. If sent, the CertificateVerify message is transmitted immediately after the Certificate message and immediately before the Finished message.

For example, if the transcript hash consists of 32 bytes having the value 01, the content covered by the signature in server Alice’s CertificateVerify message reads like this:

2020202020202020202020202020202020202020202020202020202020202020
2020202020202020202020202020202020202020202020202020202020202020
544c5320312e332c207365727665722043657274696669636174655665726966
79
00
0101010101010101010101010101010101010101010101010101010101010101

The sender of the CertificateVerify message computes the signature by taking the following data as input:

• The data covered by the signature
• The private key corresponding to the public key in the sender’s certificate transmitted in the previous TLS message

When server Alice sends the CertificateVerify message, the digital signature algorithm Alice uses must be one of the algorithms that client Bob specified in his signature˙algorithms extension.

When client Bob sends the CertificateVerify message, the digital signature algorithm must be among those specified in the supported˙signature˙algorithms field of the signature˙algorithms extension in the CertificateRequest message.

The above illustrates how TLS addresses potential compatibility issues in a heterogeneous environment where different clients must communicate with different servers, with the endpoints likely supporting different digital signature algorithms.

The receiver of the CertificateVerify message verifies the digital signature. The verification process takes the following data as input:

• The data covered by the signature
• The public key in the certificate from the corresponding Certificate message
• The digital signature in the received CertificateVerify message

If the verification is not successful, the receiver terminates the TLS handshake and sends a decrypt˙alert alert to the other communicating party.

10.5.12 The certificate_authorities extension

Finally, we turn to certificate authorities within TLS. TLS in itself places hardly any requirement on CAs, except that they should be able to issue X.509 certificates. However, Alice and Bob can use the certificate˙authorities extension to specify which certification authorities they support and which should be used by the receiving TLS party to select the appropriate certificates.

Client Bob sends the certificate˙authorities extension in his ClientHello message. Server Alice sends the certificate˙authorities extension in her CertificateRequest message. certificate˙authorities contains the CertificateAuthoritiesExtension data structure, as shown in Listing 10.8.

Listing 10.8: CertificateAuthoritiesExtension data structure

opaque DistinguishedName<1..2^16-1>;

struct {
   DistinguishedName authorities<3..2^16-1>;
} CertificateAuthoritiesExtension;

In CertificateAuthoritiesExtension, field authorities holds a list of the distinguished names of suitable CAs. The CA names are represented in the DER-encoded format. The authorities variable also contains the name of the trust anchor or the subordinate CA. As a result, server Alice and client Bob can use the certificate˙authorities extension to specify the known trust anchors as well as the preferred authorization space.

10.6 Summary

In this chapter, we have discussed digital certificates as a means to provide authenticity for public keys, and the bodies that issue certificates, Certification Authorities (CAs). In particular, we looked at the minimum set of data that needs to be presented within a certificate, and the optional parts of a certificate.

Regarding CAs, we discussed their tasks and the processes for obtaining and validating certificates. We have also seen how CAs fit into the larger structure needed to manage public keys, the Public-Key Infrastructure (PKI).

After these more general considerations, we looked in detail at how digital certificates are handled within the TLS 1.3 handshake protocol.

The next chapter will be more technical again, as it discusses hash functions and message authentication codes. Apart from digital signatures (which also use hash functions), they are the main cryptographic mechanisms for providing authenticity to handshake messages.

11.1 The need for authenticity and integrity

Imagine Alice being a control computer in a train control system and Bob being a board computer installed within a train. For a more realistic scenario, let’s assume the train control system is a positive train control. This means that the train is only allowed to move if it receives an explicit move message from the train control. Otherwise, the train does not move.

Further, assume that there are two different move messages that onboard computer Bob can receive from control computer Alice:

• Message ms instructing the train to move slowly, for example, before entering a train station
• Message mf instructing the train to move fast

In addition, to secure the train control against cyberattacks, the communication channel between Alice and Bob is protected using a cryptographic mechanism that provides confidentiality only. That is, Alice and Bob share a secret key k and can compute an encryption function ek to make their communication unintelligible to the attacker, Mallory. However, they have no means to detect manipulation of the encrypted messages. The setup is illustrated in Figure 11.1.

Now, while Mallory cannot read the clear text communication between Alice and Bob, she can record and manipulate the encrypted messages. So, when Alice sends Bob the message ek(mf), Mallory simply changes it to the message ek(ms). Upon receiving the manipulated message, Bob decrypts it and obtains ms. Because ms is a legitimate message in the train control system, the onboard computer Bob accepts it and makes the train go slower than it is supposed to go, resulting in a delay at the next train station.

In cryptographic terms, the above attack works because Bob cannot verify the integrity of the message he received. After decrypting the message, Bob can determine whether it is in principle a valid train control message, but he has no way to check if it was manipulated en route.

Figure 11.1: Example setting ensuring confidentiality, but not integrity and authenticity

Next, imagine a scenario where the train is halted for safety reasons, say, waiting for another train coming from the opposite direction to pass. Since our example is a positive train control, no messages are sent by the control computer Alice to the onboard computer Bob and, as a result, the train remains halted. What happens if Mallory sends the message ek(ms) to Bob?

Upon receiving ek(ms), Bob decrypts it and obtains the clear text message ms telling the train to move slowly. Again, ms is a valid message in the train control system and so is processed by onboard computer Bob. The train is set in motion and, as a result, causes an accident if there is no human operator in the loop to react in a timely way.

From the cryptographic perspective, the above attack is possible because Bob cannot verify the authenticity of the received message ek(ms). While he can check that the plain text message ms is a valid message, Bob cannot determine whether it was actually sent by Alice or by someone else. In other words, Bob is not able to verify the origin of the message. Moreover, there is no way for Bob to verify the freshness of the message, which opens up further attack possibilities for Mallory (this was already discussed earlier, in Section 2.5, Authentication in Chapter 2, Secure Channel and the CIA Triad).

11.2 What cryptographic guarantees does encryption provide?

On a more fundamental level, the attacks described in the above examples work because Alice and Bob, as illustrated in Figure 11.1, can only use encryption ek.

Intuitively, it might seem as if encryption protects Alice’s and Bob’s messages against manipulation by Mallory because the ciphertext hides the plaintext message and Mallory cannot know how to manipulate the encrypted message in a meaningful way. But this is completely wrong! Encryption provides no guarantees for message integrity or authenticity.

We can convince ourselves that this is indeed the case by taking a closer look at the one-time pad encryption scheme from Chapter 4, Encryption and Decryption.

Recall that the one-time pad encrypts a message m under the key k as:

where ⊕ denotes a bit-wise exclusive OR (XOR) operation. If you take two bits b0,b1 and apply the XOR operation to them, b0 ⊕ b1 will yield zero whenever both bits have the same value (that is, both are zero or both are one) and one whenever the bits have a different value.

To decrypt a message encrypted under the one-time pad scheme, the receiver computes:

In the case a one-time pad is used, it is very easy for Mallory to manipulate the ciphertext c because every bit flip in the ciphertext leads to the same bit being flipped in the decrypted message.

In other words, if Mallory has a ciphertext c that encrypts Bob’s message m, she can easily generate a manipulated ciphertext c′ that encrypts the same message as m, but with one or more bits of Mallory’s choice flipped.

Thus, even a perfectly secret – that is, information-theoretically secure – encryption scheme does not provide message integrity. The same is true for stream ciphers because, as we have seen in Chapter 4, Encryption and Decryption, their encryption operation is identical to encryption using the one-time pad: the plaintext is simply XORed with the key stream.

Intuitively, one might think that block ciphers – a class of much stronger encryption algorithms we will learn about in Chapter 14, Block Ciphers and Their Modes of Operation – are resilient against the above manipulations and would offer some degree of integrity. After all, modern block ciphers are pseudorandom permutations where a one-bit change in the plaintext results in the change of roughly half of the bits in the ciphertext.

As a result, if Mallory changes only a single bit in ciphertext c to obtain a manipulated ciphertext c′, the decryption result p′ = dk(c′) will be totally different from the genuine decryption result p = dk(c). It turns out, however, that even this property does not help with message integrity and authenticity!

As an example, if a block cipher is used in the so-called electronic codebook (ECB) mode (more on this in Chapter 14, Block Ciphers and their Modes of Operation) and Mallory flips a bit in the i-th block of the ciphertext, only the i-th block of the plaintext will change when Bob decrypts the manipulated ciphertext.

Alternatively, Mallory can manipulate the order of blocks in the original ciphertext c to obtain a manipulated ciphertext c′. When Bob decrypts c′, he will obtain a manipulated plaintext p′ where the individual blocks are identical to those of the genuine plaintext p, but their order is manipulated (their order is the same as in c′).

If only encryption is used, Bob is not able to detect these manipulations. Moreover, this is independent of the type of symmetric key encryption algorithm used by Bob. We can therefore conclude that encryption alone provides only confidentiality, but not message integrity or authenticity.

11.4.2 One-way property

In Chapter 5, Entity Authentication, we showed how passwords can be stored in a secure way on a server using hash functions. More specifically, each password is hashed together with some random value (the salt) and the hash value is stored together with the corresponding user ID. This system can only be secure if it is computationally difficult to invert the hash function, that is, to find a matching input for a known output. The same requirement emerges if the hash function is used in a key-dependent way in order to form a MAC (see Section 11.5, Message authentication codes).

In order to put this requirement in a more precise way, we only need to apply our earlier definition of a one-way function from Section 11.3, One-way functions, to hash functions:

A hash function hash is said to be one-way or preimage resistant, if it is computationally infeasible to find an input m for a given output y so that y = hash(m).

As is the case for second preimages, preimages for a given n-bit output will occur automatically after O(2n) trial inputs. Hash functions that are preimage resistant and second preimage resistant are called one-way hash functions (OWHF).

11.4.3 Merkle-Damgard construction

Our previous discussion of requirements on a secure hash function shows that in order to achieve collision resistance, it is important that all input bits have an influence on the hash value. Otherwise, it would be very easy to construct collisions by varying the input bits that do not influence the outcome.

How can we accommodate this requirement when dealing with inputs m of indeterminate length? We divide m into pieces (or blocks) of a fixed size, then you deal with the blocks one after the other. In one construction option, the block is compressed, that is mapped onto a smaller bit string, which is then processed together with the next block.

The Merkle-Damgard scheme has been the main construction principle for cryptographic hash functions in the past. Most importantly, the MD5 (128-bit hash), SHA-1 (160-bit hash), and SHA-2 (256-bit hash) hash functions are built according to this scheme. Later in this chapter, in Section 11.7, Hash functions in TLS, we will look at the SHA-family of hash functions in detail, as these functions play an important role within TLS.

For now, we’ll concentrate on the details of the Merkle-Damgard scheme. In order to compute the hash value of an input message m of arbitrary length, we proceed according to the following steps:

• Separate message m into k blocks of length r, using padding if necessary. In the SHA-1 hash function, input messages are always padded by a 1 followed by the necessary number of 0-bits. The block length of SHA-1 is r = 512.
• Concatenate the first block m1 with an initialization vector IV of length n.
• Apply a compression function comp : {0,1}n+r → {0,1}n on the result, to get

• Process the remaining blocks by computing

Note that each hi has length n.

• Set

Note that finding a collision in comp implies a collision in hash. More precisely, if we can find two different bit strings y1,y2 of length r so that comp(x||y1) = comp(x||y2) for some given n−bit string x, then we can construct two different messages m,m with the same hash value:

The article [8] lists a number of generic attacks on hash functions based on the Merkle-Damgard scheme. Although in most cases these attacks are far from being practical, they are still reason for concern about the general security of the scheme.

11.4.4 Sponge construction

Sponge construction is used in the formulation of the SHA-3 standard hash algorithm Keccak [26]. It works by first absorbing the input message into some state vector →S (the sponge). After one block has been absorbed, the state vector is permuted to achieve a good mixing of the input bits. After all input blocks have been processed, the n bits of the hash value are squeezed out of the sponge.

The detailed construction is as follows:

1. Separate message m into k blocks of length r.
2. Form the first state vector →S0 = 0b, that is, a string consisting of b 0’s, where b = 25 × 2l, and b > r.
3. Absorb: For each message block, modify state vector →Si−1 by message block mi and permute the result via some bijective round function f : {0,1}b → 0,1b:

The final result is a b-bit vector →Sk, into which the message blocks have been absorbed.

4. Squeeze: We are now squeezing n bit out of the state vector →Sk.

If n < r, we simply take the first n bit of →Sk:

Otherwise, we form the following string of length (12 + 2l + 1) × r by repeatedly applying the round function f on →Sk:

Afterward, we pick the first n bits again:

We will now see how hash functions are used to form Message Authentication Codes (MACs).

11.5 Message authentication codes

If Alice wants to securely transmit a message m to Bob, she must use a so-called Message Authentication Code (MAC) to prevent Eve from tampering with that message. More precisely, a MAC prevents Mallory from doing the following:

• Modifying m without Bob noticing it
• Presenting Bob a message m′ generated by Mallory, m′≠m, without Bob noticing that m′ was not sent by Alice

Therefore, a MAC helps us to achieve the two security objectives integrity protection and message authentication (see Chapter 2, Secure Channel and the CIA Triad and Chapter 5, Entity Authentication). Note that a MAC cannot prevent the tampering itself, nor can it prevent message replay. The active attacker Mallory can always manipulate the genuine message m, or present Bob with the message m′ and pretend that it was sent by Alice. A MAC only gives Bob the ability to detect that something went wrong during the transmission of the message he received. Bob cannot reconstruct the genuine message m from a MAC. In fact, he cannot even determine whether the wrong MAC results from an attack by Mallory or from an innocuous bit flip caused by a transmission error. Later in this chapter, we will see that this property has fundamental implications on the use of MACs in safety-critical systems.

If Alice and Bob want to secure their messages with MACs, they need to share a secret k in advance. Once the shared secret is established, Alice and Bob can use MACs as illustrated in Figure 11.2. The sender Alice computes the MAC t as a function of her message m and the secret key k she shares with Bob. She then appends t to message m—denoted by m∥t—and sends the result to Bob. Upon receiving the data, Bob uses the message m, the MAC t, and the shared secret k to verify that t is a valid MAC on message m.

Figure 11.2: Working principle of MACs

So how are MACs actually computed?

11.5.1 How to compute a MAC

Basically, there are two options to form a MAC. The first option closely follows the approach we adopted to compute digital signatures in Chapter 9, Digital Signatures. Back then, we hashed the message m first and encrypted the hash value with the signer’s private key:

Analogously, using their shared secret k, Alice and Bob could compute

as MAC. Here, encryption is done via some symmetric encryption function, for example, a block cipher (see Chapter 14, Block Ciphers and Their Modes of Operation). Note that if Alice sends m||t to Bob and Eve manages to find another message m so that hash(m) = hash(m), then Eve can replace m with m without being noticed. This motivates the collision resistance requirement on hash functions described in Section 11.4, Hash functions.

However, even if we are using a collision-resistant hash function, in a symmetric setting where Alice and Bob both use the same key k, one might ask whether it is really necessary to agree on and deploy two different kinds of algorithms for computing a MAC. Moreover, hash functions are built for speed and generally have a much better performance than block ciphers.

The second option for computing a MAC therefore only uses hash functions as building blocks. Here, the secret k is used to modify the message m in a certain way and the hash function is applied to the result:

This option is called a key-dependent hash value. In which way k should influence the message m, depends on how the hash function is constructed. In any case, if Eve is able to reconstruct the input data from the output value hash(m,k), she might be able to get part of or even the complete secret key k. This motivates the one-way property requirement on hash functions described in Section 11.4, Hash functions. A well-proven way to construct a key-dependent hash called HMAC is defined in [103].

11.5.2 HMAC construction

The HMAC construction is a generic template for constructing a MAC via a key-dependent hash function. In this construction, the underlying hash function hash is treated as a black box that can be easily replaced by some other hash function if necessary. This construction also makes it easy to use existing implementations of hash functions. It is used within TLS as part of the key derivation function HKDF (see Section 12.3, Key derivation functions in TLS within Chapter 12, Key Exchange).

When looking at the way hash functions are built, using either the Merkle-Damgard or the Sponge Construction, it quickly becomes clear that input bits from the first message blocks are well diffused over the final output hash value. Input bits in the last message blocks, on the other hand, are only processed at the very end and the compression or the round function, respectively, is only applied a few times on these bits. It is therefore a good idea to always append the message to the key in key-dependent hash functions. The simple construction

however, suffers from so-called Hash Length Extension Attacks, if the hash function is constructed according to the Merkle-Damgard scheme. Here, an attacker knowing a valid pair (m,MACk(m)) can append another message mA to the original message m and compute the corresponding MAC without knowing the secret key k. This is because

where comp is the compression function used for building the hash function.

In the HMAC construction, the input message m is therefore appended twice to the keying material, but the second time in a hashed form that cannot be forged by an attacker. More specifically, for an input message m and a symmetric key k, we have

where:

• hash : {0,1}∗ → {0,1}n is some collision-resistant OWHF, which processes its input in blocks of size r.
• k is the symmetric key. It is recommended that the key size should be ≥ n. If k has more than r bits, one should use hash(k) instead of k.
• k′ is the key padded with zeros so that the result has r bits.
• opad and ipad are fixed bitstrings of length r: opad = 01011100 repeated r∕8 times, and ipad = 00110110 repeated r∕8 times. Both opad and ipad, when added via ⊕, flip half of the key bits.

In this construction, the hash length extension attack will not work, because in order to forge MACk(m||mA), an attacker would need to construct hash(k′⊕ ipad||m||mA). This is impossible, however, as the attacker does not know hash(k′⊕ ipad||m).

More generally, the HMAC construction does not rely on the collision-resistance of the underlying hash function, because a collision in the hash function does not imply the construction of a colliding HMAC.

SHA-256, SHA-384, and SHA-512 hash functions

SHA-256, SHA-384, and SHA-512 are hash algorithms from the Secure Hash Algorithm-2 (SHA-2) family. The algorithms are defined in FIPS 180-4, Secure Hash Standard (SHS) [129], the standard specifying NIST-approved hash algorithms for generating message digests, and are based on the Merkle-Damgard construction.

The suffix of the SHA-2 algorithms denotes the length of the message digest in bits [140]. As an example, the message digest of SHA-256 has a length of 256 bits. Table 11.1 summarizes the message size, block size, and digest size of all SHA-2 hash family algorithms.

Algorithm.	Message size (bits)	Block size (bits)	Digest size (bits)
SHA-1	< 264	512	160
SHA-224	< 264	512	224
SHA-256	< 264	512	256
SHA-384	< 2128	1024	384
SHA-512	< 2128	1024	512
SHA-512/224	< 2128	1024	224
SHA-512/256	< 2128	1024	256

 Table 11.1: Basic properties of SHA-2 hash family algorithms

All SHA-2 hash algorithms use a set of similar basic functions, only with different lengths of input and output. Every SHA-2 algorithm uses the following functions where x,y, and z are either 32-bit or 64-bit values, ⊕ denotes exclusive-OR, and ∧ denotes bitwise AND:

• Ch(x,y,z) = (x ∧ y) ⊕ (¬x ∧ z)
• Maj(x,y,z) = (x ∧ y) ⊕ (x ∧ z) ⊕ (y ∧ z)

SHA-256 functions

In addition to the preceding functions, SHA-256 uses four logical functions. Each function is applied to a 32-bit value x and outputs a 32-bit result:

∑ 0256(x) = ROTR2(x) ⊕ ROTR13(x) ⊕ ROTR22(x)

∑ 1256(x) = ROTR6(x) ⊕ ROTR11(x) ⊕ ROTR25(x)

σ0256(x) = ROTR7(x) ⊕ ROTR18(x) ⊕ SHR3(x)

σ1256(x) = ROTR17(x) ⊕ ROTR19(x) ⊕ SHR10(x)

In the preceding functions, ROTRn(x) denotes a circular right-shift operation applied to a w-bit word x, using an integer 0 ≤ n < w, defined as (x ≫ n) ∨ (x ≪ w −n), and SHRn(x) denotes a right-shift operation applied to a w-bit word x, using an integer 0 ≤ n < w, defined as x ≫ n.

SHA-512 functions

Similar to SHA-256, SHA-384 and SHA-512 also use four logical functions. However, the functions are applied to a 64-bit value x and output a 64-bit result:

∑ 0512(x) = ROTR28(x) ⊕ ROTR34(x) ⊕ ROTR39(x)

∑ 1512(x) = ROTR14(x) ⊕ ROTR18(x) ⊕ ROTR41(x)

σ0512(x) = ROTR1(x) ⊕ ROTR8(x) ⊕ SHR7(x)

σ1512(x) = ROTR19(x) ⊕ ROTR61(x) ⊕ SHR6(x)

SHA-256 constants

SHA-256 uses 64 32-bit constants K0256,K1256,…,K63256 that are the first 32 bits of the fractional parts of cube roots of the first 64 prime numbers.

SHA-384 and SHA-512 constants

SHA-384 and SHA-512 use 80 64-bit constants K0512,K1512,…,K79512 that are the first 64 bits of the fractional parts of cube roots of the first 80 prime numbers.

Preprocessing the message

All hash functions in the SHA-2 family preprocess the message before performing the actual computation. The preprocessing consists of three steps:

1. Padding the plaintext message to obtain a padded message that is a multiple of 512 bits for SHA-256 and a multiple of 1,024 bits for SHA-384 and SHA-512.
2. Parsing the message into blocks.
3. Setting the initial hash value H(0).

For SHA-256, the padded message is parsed into N 512-bit blocks M1,M2,…,MN. Because every 512-bit input block can be divided into 16 32-bit words, the input block i can be expressed as M0i,M1i,…,M1i5 where every Mji has the length of 32 bits.

Similarly, for SHA-384 and SHA-512, the padded message is parsed into N 1,024-bit blocks M1,M2,…MN. Because a 1024-bit input block can be divided into 16 64-bit words, the input block i can be expressed as M0i,M1i,…,M1i5 where every Mji has the length of 64 bits.