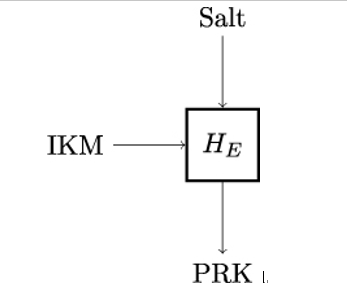
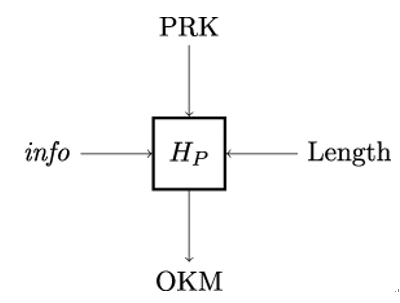
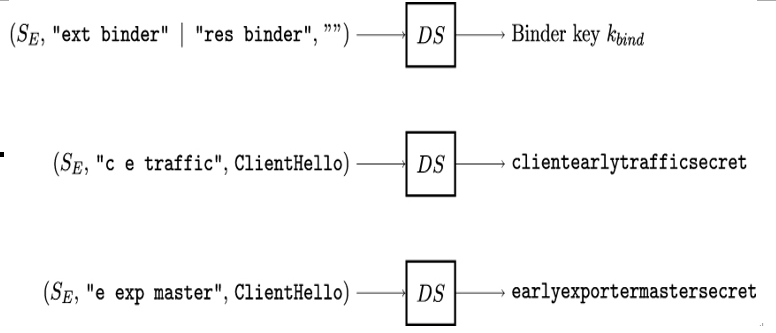
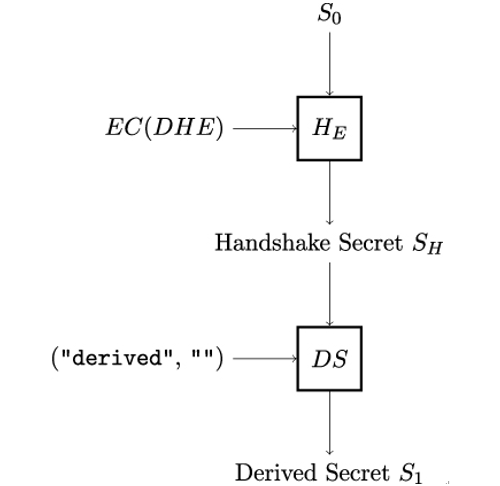
11.6 MAC versus CRC

Can we construct a MAC without a cryptographic hash function and without a secret key? Let’s take a look at the Cyclic Redundancy Check (CRC), which is popular error-detecting code used in communication systems to detect accidental errors in messages sent over a noisy or unreliable communication channel.

The working principle of error-detecting code is for the sender to encode their plaintext message in a redundant way. The redundancy, in turn, allows the receiver to detect a certain number of errors – that is, accidental bit flips – in the message they receive. The theory of channel coding, pioneered in the 1940s by the American mathematician Richard Hamming, aims to find code that has minimal overhead (that is, the least redundancy) but, at the same time, has a large number of valid code words and can correct or detect many errors.

CRC is so-called cyclic code, that is, a block code where a circular shift of every code word yields another valid code word. The use of cyclic code for error detection in communication systems was first proposed by the American mathematician and computer scientist Wesley Peterson in 1961.

Cyclic code encodes the plaintext message by attaching to it a fixed-length check value based on the remainder of a polynomial division of the message’s content. The receiving party repeats that calculation and checks whether the received check value is equal to the computed check value.

The algebraic properties of cyclic code make it suitable for efficient error detection and correction. Cyclic code is simple to implement and well suited to detect so-called burst errors. Burst errors are contiguous sequences of erroneous bits in communication messages and are common in many real-world communication channels.

CRC code is defined using a generator polynomial g(x) with binary coefficients 0 and 1. The plaintext message, encoded as another polynomial m(x), is divided by the generator polynomial. The CRC is then computed by discarding the resulting quotient polynomial and taking the remainder polynomial r(x) as CRC, which is subsequently appended to the plaintext as a checksum. The whole arithmetic is done within the finite field 𝔽2, therefore the coefficients of the remainder polynomial are also 0 and 1.

As an example, we can compute an 8-bit CRC using the generator polynomial g(x) = x2 + x + 1. To encode a message, we encode it as a polynomial, divide it by the generator polynomial x2 + x + 1, and take the remainder of this division as the CRC check value to be appended to the plaintext message.

Setting the initial hash value

Before the actual hash computation can begin, the initial hash value H0 must be set based on the specific hash algorithm used. For SHA-256, H(0) is composed of the following 8 32-bit words – denoted H0(0) to H7(0) – which are the first 32 bits of the fractional parts of the square roots of the first 8 prime numbers:

H0(0) = 6a09e667

H1(0) = bb67ae85

H2(0) = 3c6ef372

H3(0) = a54ff53a

H4(0) = 510e527f

H5(0) = 9b05688c

H6(0) = 1f83d9ab

H7(0) = 5be0cd19

For SHA-384, H(0) is composed of eight 64-bit words denoted H0(0) to H7(0), the words being the first 64 bits of the fractional parts of the square roots of the ninth through sixteenth prime numbers:

H0(0) = cbbb9d5dc1059ed8

H1(0) = 629a292a367cd507

H2(0) = 9159015a3070dd17

H3(0) = 152fecd8f70e5939

H4(0) = 67332667ffc00b31

H5(0) = 8eb44a8768581511

H6(0) = db0c2e0d64f98fa7

H7(0) = 47b5481dbefa4fa4

For SHA-512, H(0) is composed of the 8 64-bit words – denoted H0(0) to H7(0) – which are the first 64 bits of the fractional parts of the square roots of the first 8 prime numbers:

H0(0) = 6a09e667f3bcc908

H1(0) = bb67ae8584caa73b

H2(0) = 3c6ef372fe94f82b

H3(0) = a54ff53a5f1d36f1

H4(0) = 510e527fade682d1

H5(0) = 9b05688c2b3e6c1f

H6(0) = 1f83d9abfb41bd6b

H7(0) = 5be0cd19137e2179

The way the constants for the initial hash value H(0) were chosen for the SHA-2 family hash algorithms – namely, by taking the first 16 prime numbers, computing a square root of these numbers, and taking the first 32 or 64 bits of the fractional part of these square roots – is yet another example of nothing-up-my-sleeve numbers.

Because prime numbers are the atoms of number theory and the square root is a simple, well-known operation, it is very unlikely that these constants were chosen for any specific reason.

The choice of the constants is natural and their values are limited because only the first 16 prime numbers are used. As a result, it is very unlikely that someone could design a cryptographic hash function containing a backdoor based on these constants.

Message digest computation

Recall that for SHA-256, the message is first padded to have a length that is a multiple of 512. To compute the SHA-256 message digest, the message is parsed into N 512-bit blocks M(1),M(2),…M(N) is processed as shown in Algorithm 1.

The term Mt(i) denotes specific 32 bits of the 512-bit block M(i). As an example, M0(i) denotes the first 32 bits of block M(i), M1(i) denotes the next 32 bits of block M(i), and so on, up to M15(i). Moreover, the SHA-256 algorithm uses a so-called message schedule consisting of 64 32-bit words W0 to W63, 8 32-bit working variables a to h, and 2 temporary variables T1,T2. The algorithm outputs a 256-bit hash value composed of 8 32-bit words.

Computation of the SHA-512 message digest, shown in Algorithm 2, is identical to that of SHA-256, except that the message schedule consists of 80 64-bit words W0 to W79 and the algorithm uses 8 64-bit working variables a to h and outputs a 512-bit message digest composed of 8 64-bit words.

Moreover, the term Mt(i) now denotes specific 64 bits of the 1,024-bit block M(i). That is, M0(i) denotes the first 64 bits of block M(i), M1(i) denotes the next 64 bits of block M(i), and so on, up to M15(i).

Finally, the SHA-384 hash algorithm is computed exactly like SHA-512, except the following:

• The initial hash value H(0) for SHA-384 is used
• The final hash value H(N) is truncated to H0(N)|| H1(N)|| H2(N)|| H3(N)|| H4(N)|| H5(N) to produce a 384-bit message digest

Algorithm 1: Computation of the SHA-256 message digest.

Algorithm 2: Computation of the SHA-512 message digest

12.1 Key establishment in TLS 1.3

Using the TLS handshake protocol, Alice and Bob negotiate the cryptographic algorithms and key sizes. They also exchange the key shares that are required to establish the master secret. Further context-specific shared secrets and keys are then derived from this master secret according to TLS 1.3’s key derivation schedule. The secure communication channel is based on a subset of these derived secret keys.

The basic principle of TLS key establishment is shown in Figure 12.1. First, Alice and Bob negotiate cryptographic algorithms, key sizes, and exchange key shares. In the second step, Alice and Bob derive a number of context-specific TLS secrets, and in particular, a shared master secret. Each secret depends on the keying material as well as the label and the context used as inputs to generate that secret.

Finally, in the third step, Alice and Bob use the TLS secrets to derive a number of keys according to TLS 1.3’s key derivation schedule. Because the derived TLS secrets are context-specific, no further labels or additional information is needed to derive the TLS keys. However, due to context-specific secrets as input for the key derivation, the secret TLS keys are also context-specific:

Figure 12.1: A high-level view of key establishment in TLS 1.3

We will cover each of the three steps shown in Figure 12.1 in detail. As we have seen, the first step, exchange of key shares and establishment of a shared master secret over an insecure channel, can only be accomplished using a good deal of math, which is explained in Chapter 7, Public-Key Cryptography. In the present chapter, we will focus on TLS 1.3’s key derivation schedule, that is, the process of deriving further, context-specific secrets and keys from an initial secret.

12.2 TLS secrets

We saw in Chapter 3, A Secret to Share, that a good cryptographic system has multiple keys so that every key is used for a single purpose only. TLS is no exception, and in this chapter, we are going to discuss in detail what cryptographic keys client Bob and server Alice need to establish a secure TLS channel.

However, before discussing the cryptographic keys, we first need to understand what TLS secrets are and how they are derived. TLS uses a three-step approach for generation of cryptographic keys, in which the keys are generated from the secrets:

1. Alice and Bob first establish a shared master secret.
2. They derive context-specific secrets from the master secret.
3. Finally, they derive context-specific keys from these derived secrets.

Note that there is no conceptual (or cryptographic) reason to differentiate between secrets and keys. But because the TLS 1.3 specification uses this terminology and we want to provide a trustworthy guide to this specification, we felt the need to do the same differentiation here.

Table 12.1 gives an overview of secrets used in the TLS protocol and briefly explains their purpose. Don’t worry if the sheer number of TLS secrets looks overwhelming at first.

To help you, we compiled a series of graphics illustrating how the specific TLS secrets and TLS keys are interconnected. You will find the graphics at the end of the next section, Key derivation functions in TLS. In the remainder of this section, we are going to look into every TLS secret in more detail.

Secret	Purpose
Early secret	Used to generate key material if Bob and Alice use a pre-shared key (PSK) for their TLS handshake.
Binder	Establishes a binding between the PSK and current TLS handshake.
Early traffic secret	Used by Bob to encrypt early handshake traffic if the PSK is used for the TLS handshake.
Exporter secrets	Secrets that can be used outside of the TLS protocol to derive additional secret keys for higher-layer protocols or applications running on top of TLS.
Derived secrets	Intermediate secrets used as salt arguments for deriving TLS secrets.
Handshake secret	This secret is the result of the handshake. It is either derived from the early secret in case a PSK is in place or from a Diffie-Hellman key exchange between Alice and Bob. It is used as input to generate the following two TLS secrets: Bob’s handshake traffic secret and Alice’s handshake traffic secret.
Handshake traffic secrets	Used to generate TLS handshake traffic keys, one for Bob and one for Alice.
Master secret	Used as input to generate the following two TLS secrets: Bob’s application traffic secret and Alice’s application traffic secret.
Application traffic secrets	Used to generate TLS application traffic keys. Like with handshake traffic keys, one key is for Bob and one is for Alice.
Resumption master secret	Used for session resumption.

 Table 12.1: Overview of secrets used in TLS (see also [53])

12.2.1 Early secret

TLS 1.3 offers the option for Alice and Bob to use a pre-shared secret key PSK. This is a key Alice and Bob have previously agreed on independent of TLS. If Alice and Bob use a PSK for their TLS handshake, they derive the early secret from PSK and use it as input keying material (IKM) to generate binder˙key, client˙early˙traffic˙secret, and early˙exporter˙master˙secret, which will be explained later in this chapter.

12.2.2 Binder key

The binder key is used to establish a binding between Alice’s and Bob’s pre-shared secret key and their current TLS handshake as well as between the current TLS handshake and the previous TLS handshake where that PSK was generated. In other words, Bob uses the binder to prove to Alice that he indeed knows the PSK associated with the identity known to Alice.

Alice uses the PSK binder to verify that Bob actually knows the correct PSK before actually executing a PSK-based TLS handshake. If the verification fails or Bob does not present the binder to Alice, she immediately aborts the TLS handshake. This ensures that Alice does not execute a PSK-based handshake without verifying that Bob actually knows the PSK.

By binding a previous TLS session where the binder key was generated to the current TLS handshake, this mechanism also allows Alice to implicitly verify that Bob did not suffer a man-in-the-middle attack. If Mallory managed to perform a successful man-in-the-middle attack, Alice and Bob would have a different PSK and this would prevent a subsequent TLS session resumption.

12.2.3 Bob’s client early traffic secret.

If a PSK is used for the TLS handshake, client˙early˙traffic˙secret can be used to generate a key that allows Bob to encrypt early application data in the first ClientHello message of the TLS handshake. This key is only used by Bob.

12.2.4 Exporter secrets

Exporter secrets are secrets used to derive additional secret keys for use outside of the TLS protocol. Some higher-level protocols use TLS to establish a shared secret key and afterward use TLS keying material for other protocol-specific purposes. This, in turn, requires exporting keying material to higher-layer protocols or applications as well as agreeing on the context in which that keying material will be used.

For example, the DTLS-SRTP protocol first uses Datagram-TLS (DTLS) to exchange secret keys and selects the Secure Real-Time Transport Protocol (SRTP) protection suite. Subsequently, it uses DTLS master˙secret to derive SRTP keys.

To enable this, TLS offers a mechanism called Key Material Exporter, details of which are defined in RFC 5705 [145]. The exported values are referred to as Exported Keying Material (EKM). In TLS, early˙exporter˙master˙secret and exporter˙master˙secret are examples of EKM generated at different stages of the TLS handshake.

TLS exporters have the following cryptographic properties:

• They allow Bob and Alice to export the same EKM value
• For attacker Eve who does not know the master˙secret, EKM is indistinguishable from a random number
• Bob and Alice can export multiple EKM values from a single TLS connection
• Even if Eve learns one EKM value, she learns nothing about other EKM values or the master˙secret

12.3.1 HKDF-Extract

HKDF-Extract, or HE for short, implements the first stage of the HKDF, which takes the keying material as input and extracts a fixed-length pseudorandom key K from it. In particular, it is involved in the derivation of the handshake secret SH and the master secret SM (see Figure 12.9 and Figure 12.11, respectively).

HKDF-Extract is illustrated in Figure 12.3. It takes two inputs: a salt and an input keying material (IKM). The salt is a non-secret random value. If no salt is provided, HKDF-Extract takes a string of zeros of the length equal to that of the hash function output. HKDF-Extract outputs a pseudorandom key (PRK). The PRK is calculated as PRK = HMAC-Hash(salt, IKM). Since HKDF-Extract is based on the HMAC construction, which is in turn a construction template that can use different hash functions [103], HKDF-Extract can also use different cryptographic hash functions.

Figure 12.3: HKDF-Extract function used for TLS key derivation

A new TLS secret is derived using HKDF-Extract with the current TLS secret state as salt and the PSK – established out of band or derived from the resumption˙master˙secret instance of a previous TLS session – or the DHE or ECDHE based shared secret that Alice and Bob have established during the current TLS handshake as IKM.

12.3.2 HKDF-Expand

The second stage of the HKDF function expands a PRK to a pseudorandom bit string of the desired length, which can then be used to derive secret keys. HKDF-Expand is illustrated in Figure 12.4.

HKDF-Expand takes three inputs: a pseudorandom key PRK (which must have at least the length of the output of the hash function used), an optional context and application-specific information info, and the desired length in bytes of the output keying material L.

The output of HKDF-Expand is an L-byte long Output Keying Material (OKM). The OKM is calculated by first calculating the following N values, where N is the result of the ceiling function applied to (L∕HashLen):

T(0) = empty string(zero length)

T(1) = HMAC-Hash(PRK,T(0)|info|0x01)

T(2) = HMAC-Hash(PRK,T(1)|info|0x02)

 …

T(N) = HMAC-Hash(PRK,T(N − 1)|info|N)

where | denotes the bit-wise concatenation. The HMAC construction for key-dependent hash values is explained in Section 11.5, Message authentication codes. After that, the OKM is built by taking the first L octets of T = T(1)|T(2)|…|T(N).

Figure 12.4: The HKDF-Expand function HP

After each invocation of the HKDF-Extract function, the HKDF-Expand function is invoked one or more times.

Next, Alice and Bob compute the binder key kbind, client˙early˙traffic˙secret and early˙exporter˙master˙secret as shown in Figure 12.8. The binder key may be used to establish subsequent TLS sessions, and the early traffic secret and the exporter Master Secret are used to calculate the corresponding keys.

Figure 12.8: Derivation of TLS binder key, client early traffic secret and early exporter master secret

To prevent Alice and Bob from mixing up the binder keys, different labels are used for the derivation of the corresponding TLS secrets. For binder keys provisioned outside of TLS, the label ”ext binder” is used. For resumption keys provisioned as the resumption Master Secret of a previous handshake, the label ”res binder” is used.

If Alice and Bob choose to perform the TLS handshake based on a PSK, there are multiple possible values that the early secret SE can take. The actual value of SE depends on the PSK that Alice selects from those offered by Bob (using their identifiers).

As a result, Bob needs to compute the early secret for every PSK he offers to Alice. If Alice selects no PSK from those being offered by Bob, he needs to compute the early secret with a PSK being all zeros.

In the next step, illustrated in Figure 12.9, Alice and Bob compute the Handshake Secret SH and the second intermediate secret S1. The Handshake Secret is derived from the first intermediate secret S0 and the DHE or ECDHE key share that Alice and Bob exchange during the TLS handshake.

Figure 12.9: Derivation of the TLS handshake secret SH and the second derived secret S1

In the fourth step, Alice and Bob derive the client˙handshake˙traffic˙secret and server˙handshake˙traffic˙secret secrets needed to compute the corresponding handshake traffic keys. This is shown in Figure 12.10.

Note how – in addition to using the handshake secret SH itself – the handshake traffic secrets are derived using not only the ”c hs traffic” and c—”s hs traffic”— labels but also the transcript transCHSH of all TLS handshakes starting with ClientHello up until and including the ServerHello message.

Figure 12.10: Derivation of TLS handshake traffic secrets

Next, as shown in Figure 12.11, Alice and Bob derive the master secret SM. This secret will be used for the calculation of the application traffic keys for protecting the bulk application data Alice and Bob want to transmit over the secure TLS channel.

Figure 12.11: Derivation of the TLS master secret

While the early secret, handshake secret, and master secret (as well as the two intermediate derived secrets) can be viewed as raw entropy without any context, traffic secrets and exporter secrets include the TLS handshake context and, as a result, can be used to derive cryptographic keys without any additional context information.

Moreover, multiple invocations of the Derive-Secret function DS take the same TLS secret as input but return different outputs because they take different messages as additional input argument.

Finally, the master secret SM, the corresponding labels and the TLS handshake transcript transCHSF are used to derive the first application traffic secrets, the exporter master secret and the resumption master secret (see Figure 12.12). Transcript transCHSF includes all handshake messages starting from ClientHello up until including the Alice’s Finished message.

Figure 12.12: Derivation of the TLS application traffic secrets, exporter master secret and resumption master secret

This step concludes the derivation of TLS secrets from the keying material. However, the secrets may be updated without having to exchange new key material.