11.4 Hash functions

A hash function is some function hash that maps an arbitrarily long input string onto an output string of fixed length n. More formally, we have hash : {0,1}∗→{0,1}n.

A simplistic example of a hash function would be a function that always outputs the last n bits of an arbitrary input string m. Or, if n = 1, one could use the bitwise XOR of all input bits as the hash value.

However, these simple hash functions do not possess any of the properties required from a cryptographically secure hash function. We will now first discuss these properties, and afterward look at how secure hash functions are actually constructed.

11.4.1 Collision resistance

Cryptographic hash functions are hard to construct because they have to fulfill stringent requirements, which are motivated by their use within Message Authentication Codes (MACs) (see Section 11.5, Message Authentication Codes) and Digital Signatures (see Chapter 9, Digital Signatures).

Recall, for example, that in the RSA cryptosystem, Alice computes a digital signature over some message m as

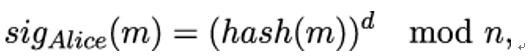
where d is Alice’s private key and n is the public module. Alice then sends the pair (m,sigAlice(m)) to Bob.

If Eve observes this pair, she can compute hash(m) using Alice’s public key PKAlice = (e,n) via

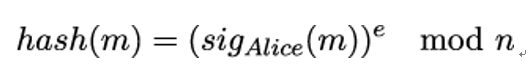
Eve now knows hash(m) and the corresponding preimage m. If she manages to find another message m with the same hash value (a so-called second preimage), m and m will have the same signature. Effectively, Eve has signed m in Alice’s name without knowing her private key. This is the most severe kind of attack on a cryptographic hash function.

Therefore, given m and hash(m), it must be computationally hard for Eve to find a second preimage m such that hash(m) = hash(m). This property of a cryptographic hash function is called second preimage resistance or weak collision resistance.

Note that when trying out different input messages for the hash function, collisions must occur at some point, because hash can map longer messages onto shorter messages. In particular, if the given hash value hash(m) is n bits long, a second preimage m should be found after O(2n) trials. Therefore a second preimage attack is considered successful only if it has a significantly smaller complexity than O(2n).

A weaker form of attack occurs if Eve manages to find any collision, that is, any two messages m1,m2 with

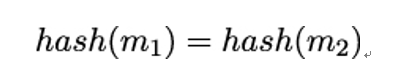
without reference to some given hash value. If it is computationally hard for Eve to construct any collisions, the hash is called strongly collision resistant.

Again, when trying out many different candidate messages, collisions will naturally occur at some point, this time after about 2n∕2 trials. This smaller number is a consequence of a phenomenon commonly known as Birthday Paradox, which we will discuss in detail in Section 19.7, Attacks on hash functions in Chapter 19, Attacks on Cryptography.

Consequently, an attack on strong collision resistance is considered successful only if it has a significantly smaller complexity than O(2n∕2). This also shows that in general, that is, assuming there are no cryptographic weaknesses, hash functions with longer hash values can be considered to be more secure than hash functions with shorter hash values.

Note that strong collision resistance of a hash function implies weak collision resistance. Hash functions that are both strongly and weakly collision resistant are called collision resistant hash functions (CRHF).