11.4.2 One-way property
In Chapter 5, Entity Authentication, we showed how passwords can be stored in a secure way on a server using hash functions. More specifically, each password is hashed together with some random value (the salt) and the hash value is stored together with the corresponding user ID. This system can only be secure if it is computationally difficult to invert the hash function, that is, to find a matching input for a known output. The same requirement emerges if the hash function is used in a key-dependent way in order to form a MAC (see Section 11.5, Message authentication codes).
In order to put this requirement in a more precise way, we only need to apply our earlier definition of a one-way function from Section 11.3, One-way functions, to hash functions:
A hash function hash is said to be one-way or preimage resistant, if it is computationally infeasible to find an input m for a given output y so that y = hash(m).
As is the case for second preimages, preimages for a given n-bit output will occur automatically after O(2n) trial inputs. Hash functions that are preimage resistant and second preimage resistant are called one-way hash functions (OWHF).
11.4.3 Merkle-Damgard construction
Our previous discussion of requirements on a secure hash function shows that in order to achieve collision resistance, it is important that all input bits have an influence on the hash value. Otherwise, it would be very easy to construct collisions by varying the input bits that do not influence the outcome.
How can we accommodate this requirement when dealing with inputs m of indeterminate length? We divide m into pieces (or blocks) of a fixed size, then you deal with the blocks one after the other. In one construction option, the block is compressed, that is mapped onto a smaller bit string, which is then processed together with the next block.
The Merkle-Damgard scheme has been the main construction principle for cryptographic hash functions in the past. Most importantly, the MD5 (128-bit hash), SHA-1 (160-bit hash), and SHA-2 (256-bit hash) hash functions are built according to this scheme. Later in this chapter, in Section 11.7, Hash functions in TLS, we will look at the SHA-family of hash functions in detail, as these functions play an important role within TLS.
For now, we’ll concentrate on the details of the Merkle-Damgard scheme. In order to compute the hash value of an input message m of arbitrary length, we proceed according to the following steps:
- Separate message m into k blocks of length r, using padding if necessary. In the SHA-1 hash function, input messages are always padded by a 1 followed by the necessary number of 0-bits. The block length of SHA-1 is r = 512.
- Concatenate the first block m1 with an initialization vector IV of length n.
- Apply a compression function comp : {0,1}n+r → {0,1}n on the result, to get
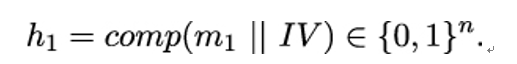
- Process the remaining blocks by computing
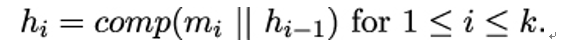
Note that each hi has length n.
- Set
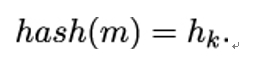
Note that finding a collision in comp implies a collision in hash. More precisely, if we can find two different bit strings y1,y2 of length r so that comp(x||y1) = comp(x||y2) for some given n−bit string x, then we can construct two different messages m,m with the same hash value:
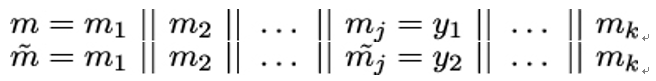
The article [8] lists a number of generic attacks on hash functions based on the Merkle-Damgard scheme. Although in most cases these attacks are far from being practical, they are still reason for concern about the general security of the scheme.