11.4.4 Sponge construction

Sponge construction is used in the formulation of the SHA-3 standard hash algorithm Keccak [26]. It works by first absorbing the input message into some state vector →S (the sponge). After one block has been absorbed, the state vector is permuted to achieve a good mixing of the input bits. After all input blocks have been processed, the n bits of the hash value are squeezed out of the sponge.

The detailed construction is as follows:

1. Separate message m into k blocks of length r.
2. Form the first state vector →S0 = 0b, that is, a string consisting of b 0’s, where b = 25 × 2l, and b > r.
3. Absorb: For each message block, modify state vector →Si−1 by message block mi and permute the result via some bijective round function f : {0,1}b → 0,1b:

The final result is a b-bit vector →Sk, into which the message blocks have been absorbed.

4. Squeeze: We are now squeezing n bit out of the state vector →Sk.

If n < r, we simply take the first n bit of →Sk:

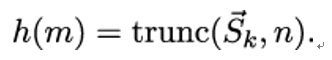
Otherwise, we form the following string of length (12 + 2l + 1) × r by repeatedly applying the round function f on →Sk:

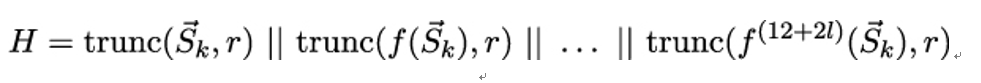
Afterward, we pick the first n bits again:

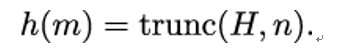
We will now see how hash functions are used to form Message Authentication Codes (MACs).

11.5 Message authentication codes

If Alice wants to securely transmit a message m to Bob, she must use a so-called Message Authentication Code (MAC) to prevent Eve from tampering with that message. More precisely, a MAC prevents Mallory from doing the following:

• Modifying m without Bob noticing it
• Presenting Bob a message m′ generated by Mallory, m′≠m, without Bob noticing that m′ was not sent by Alice

Therefore, a MAC helps us to achieve the two security objectives integrity protection and message authentication (see Chapter 2, Secure Channel and the CIA Triad and Chapter 5, Entity Authentication). Note that a MAC cannot prevent the tampering itself, nor can it prevent message replay. The active attacker Mallory can always manipulate the genuine message m, or present Bob with the message m′ and pretend that it was sent by Alice. A MAC only gives Bob the ability to detect that something went wrong during the transmission of the message he received. Bob cannot reconstruct the genuine message m from a MAC. In fact, he cannot even determine whether the wrong MAC results from an attack by Mallory or from an innocuous bit flip caused by a transmission error. Later in this chapter, we will see that this property has fundamental implications on the use of MACs in safety-critical systems.

If Alice and Bob want to secure their messages with MACs, they need to share a secret k in advance. Once the shared secret is established, Alice and Bob can use MACs as illustrated in Figure 11.2. The sender Alice computes the MAC t as a function of her message m and the secret key k she shares with Bob. She then appends t to message m—denoted by m∥t—and sends the result to Bob. Upon receiving the data, Bob uses the message m, the MAC t, and the shared secret k to verify that t is a valid MAC on message m.

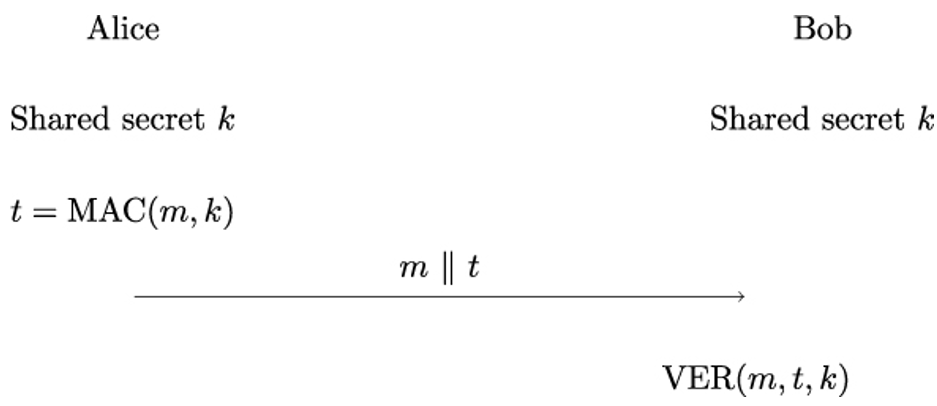
Figure 11.2: Working principle of MACs

So how are MACs actually computed?