11.5.1 How to compute a MAC
Basically, there are two options to form a MAC. The first option closely follows the approach we adopted to compute digital signatures in Chapter 9, Digital Signatures. Back then, we hashed the message m first and encrypted the hash value with the signer’s private key:
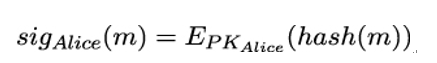
Analogously, using their shared secret k, Alice and Bob could compute
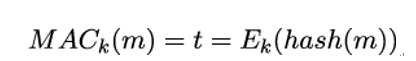
as MAC. Here, encryption is done via some symmetric encryption function, for example, a block cipher (see Chapter 14, Block Ciphers and Their Modes of Operation). Note that if Alice sends m||t to Bob and Eve manages to find another message m so that hash(m) = hash(m), then Eve can replace m with m without being noticed. This motivates the collision resistance requirement on hash functions described in Section 11.4, Hash functions.
However, even if we are using a collision-resistant hash function, in a symmetric setting where Alice and Bob both use the same key k, one might ask whether it is really necessary to agree on and deploy two different kinds of algorithms for computing a MAC. Moreover, hash functions are built for speed and generally have a much better performance than block ciphers.
The second option for computing a MAC therefore only uses hash functions as building blocks. Here, the secret k is used to modify the message m in a certain way and the hash function is applied to the result:
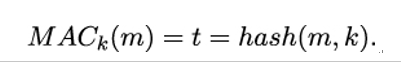
This option is called a key-dependent hash value. In which way k should influence the message m, depends on how the hash function is constructed. In any case, if Eve is able to reconstruct the input data from the output value hash(m,k), she might be able to get part of or even the complete secret key k. This motivates the one-way property requirement on hash functions described in Section 11.4, Hash functions. A well-proven way to construct a key-dependent hash called HMAC is defined in [103].
11.5.2 HMAC construction
The HMAC construction is a generic template for constructing a MAC via a key-dependent hash function. In this construction, the underlying hash function hash is treated as a black box that can be easily replaced by some other hash function if necessary. This construction also makes it easy to use existing implementations of hash functions. It is used within TLS as part of the key derivation function HKDF (see Section 12.3, Key derivation functions in TLS within Chapter 12, Key Exchange).
When looking at the way hash functions are built, using either the Merkle-Damgard or the Sponge Construction, it quickly becomes clear that input bits from the first message blocks are well diffused over the final output hash value. Input bits in the last message blocks, on the other hand, are only processed at the very end and the compression or the round function, respectively, is only applied a few times on these bits. It is therefore a good idea to always append the message to the key in key-dependent hash functions. The simple construction
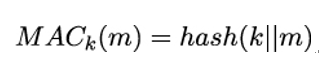
however, suffers from so-called Hash Length Extension Attacks, if the hash function is constructed according to the Merkle-Damgard scheme. Here, an attacker knowing a valid pair (m,MACk(m)) can append another message mA to the original message m and compute the corresponding MAC without knowing the secret key k. This is because
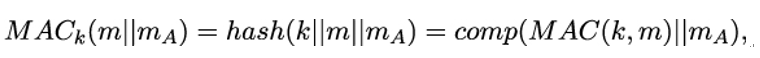
where comp is the compression function used for building the hash function.
In the HMAC construction, the input message m is therefore appended twice to the keying material, but the second time in a hashed form that cannot be forged by an attacker. More specifically, for an input message m and a symmetric key k, we have
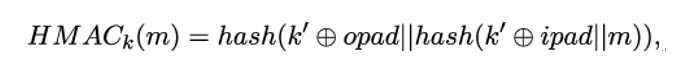
where:
- hash : {0,1}∗ → {0,1}n is some collision-resistant OWHF, which processes its input in blocks of size r.
- k is the symmetric key. It is recommended that the key size should be ≥ n. If k has more than r bits, one should use hash(k) instead of k.
- k′ is the key padded with zeros so that the result has r bits.
- opad and ipad are fixed bitstrings of length r: opad = 01011100 repeated r∕8 times, and ipad = 00110110 repeated r∕8 times. Both opad and ipad, when added via ⊕, flip half of the key bits.
In this construction, the hash length extension attack will not work, because in order to forge MACk(m||mA), an attacker would need to construct hash(k′⊕ ipad||m||mA). This is impossible, however, as the attacker does not know hash(k′⊕ ipad||m).
More generally, the HMAC construction does not rely on the collision-resistance of the underlying hash function, because a collision in the hash function does not imply the construction of a colliding HMAC.