Archives January 2021

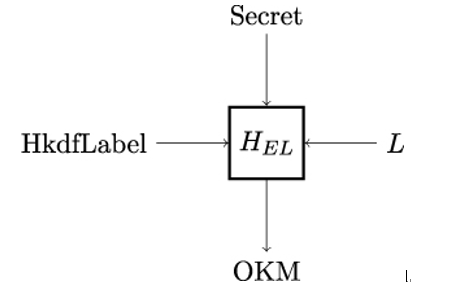
Next, Alice and Bob compute the binder key kbind, client˙early˙traffic˙secret and early˙exporter˙master˙secret as shown in Figure 12.8. The binder key may be used to establish subsequent TLS sessions, and the early traffic secret and the exporter Master Secret are used to calculate the corresponding keys.

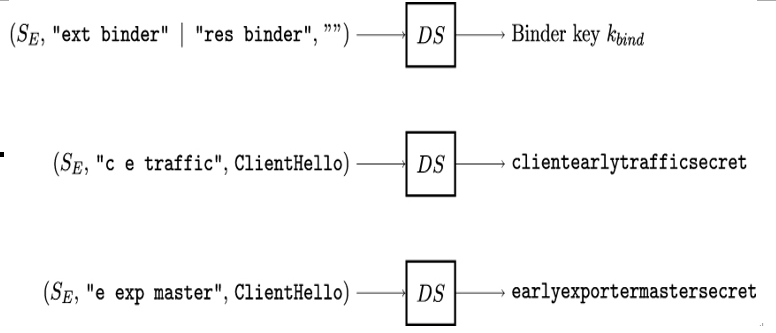
Figure 12.8: Derivation of TLS binder key, client early traffic secret and early exporter master secret

To prevent Alice and Bob from mixing up the binder keys, different labels are used for the derivation of the corresponding TLS secrets. For binder keys provisioned outside of TLS, the label ”ext binder” is used. For resumption keys provisioned as the resumption Master Secret of a previous handshake, the label ”res binder” is used.

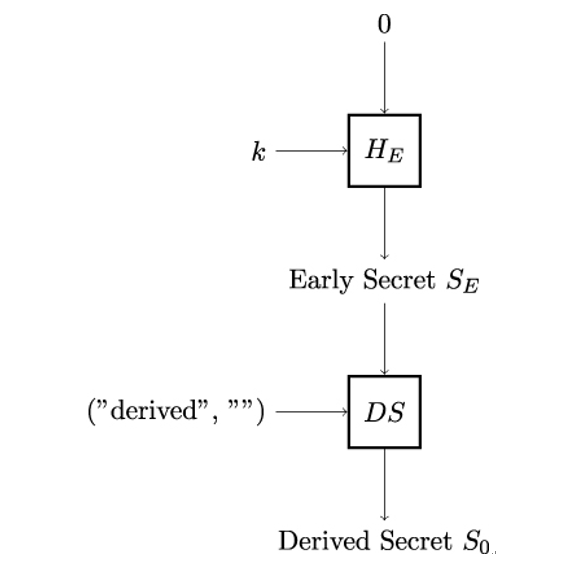
If Alice and Bob choose to perform the TLS handshake based on a PSK, there are multiple possible values that the early secret SE can take. The actual value of SE depends on the PSK that Alice selects from those offered by Bob (using their identifiers).

As a result, Bob needs to compute the early secret for every PSK he offers to Alice. If Alice selects no PSK from those being offered by Bob, he needs to compute the early secret with a PSK being all zeros.

In the next step, illustrated in Figure 12.9, Alice and Bob compute the Handshake Secret SH and the second intermediate secret S1. The Handshake Secret is derived from the first intermediate secret S0 and the DHE or ECDHE key share that Alice and Bob exchange during the TLS handshake.

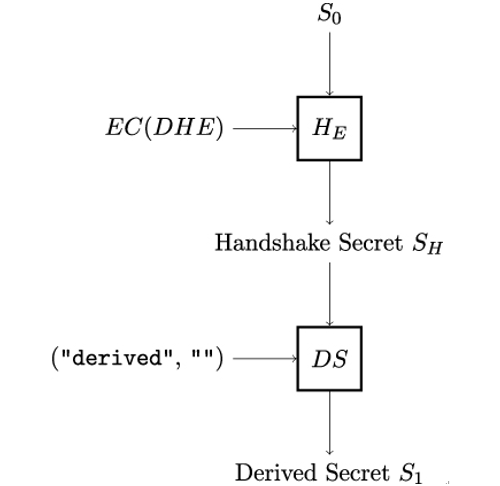
Figure 12.9: Derivation of the TLS handshake secret SH and the second derived secret S1

In the fourth step, Alice and Bob derive the client˙handshake˙traffic˙secret and server˙handshake˙traffic˙secret secrets needed to compute the corresponding handshake traffic keys. This is shown in Figure 12.10.

Note how – in addition to using the handshake secret SH itself – the handshake traffic secrets are derived using not only the ”c hs traffic” and c—”s hs traffic”— labels but also the transcript transCHSH of all TLS handshakes starting with ClientHello up until and including the ServerHello message.

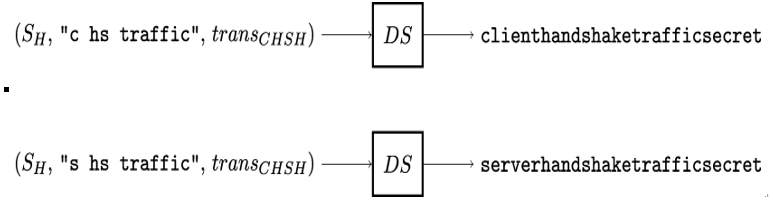
Figure 12.10: Derivation of TLS handshake traffic secrets

Next, as shown in Figure 12.11, Alice and Bob derive the master secret SM. This secret will be used for the calculation of the application traffic keys for protecting the bulk application data Alice and Bob want to transmit over the secure TLS channel.

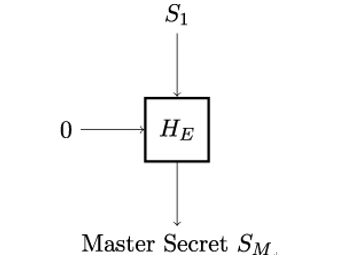
Figure 12.11: Derivation of the TLS master secret

While the early secret, handshake secret, and master secret (as well as the two intermediate derived secrets) can be viewed as raw entropy without any context, traffic secrets and exporter secrets include the TLS handshake context and, as a result, can be used to derive cryptographic keys without any additional context information.

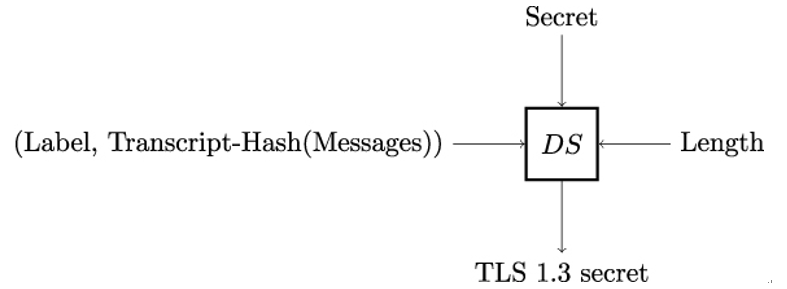
Moreover, multiple invocations of the Derive-Secret function DS take the same TLS secret as input but return different outputs because they take different messages as additional input argument.

Finally, the master secret SM, the corresponding labels and the TLS handshake transcript transCHSF are used to derive the first application traffic secrets, the exporter master secret and the resumption master secret (see Figure 12.12). Transcript transCHSF includes all handshake messages starting from ClientHello up until including the Alice’s Finished message.

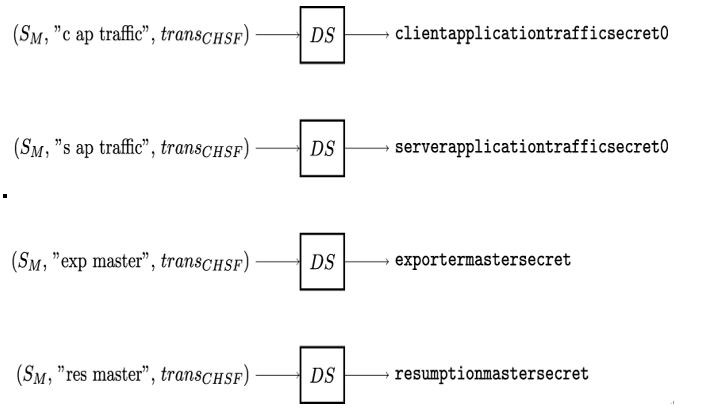
Figure 12.12: Derivation of the TLS application traffic secrets, exporter master secret and resumption master secret

This step concludes the derivation of TLS secrets from the keying material. However, the secrets may be updated without having to exchange new key material.

12.3.3 HKDF-Expand-Label

HKDF-Expand-Label (or HEL for short) is a pseudorandom function as shown in Figure 12.5. Recall this means that it can be efficiently computed for any given input, but it cannot be efficiently distinguished from a uniformly random function [37].

HKDF-Expand-Label takes a secret, the desired length of the output L, and an HKDF-Label as input, and expands them to OKM.

Figure 12.5: The HKDF-Expand-Label function HEL

The HkdfLabel data structure is defined as in Listing 12.1. It essentially consists of a label and a context. All labels used in TLS 1.3 are strings. The context might have zero length.

Listing 12.1: HkdfLabel data structure

struct {
   uint16 length = Length;
   opaque label<7..255> = “tls13 ” + Label;
   opaque context<0..255> = Context;
} HkdfLabel;

HKDF-Expand-Label illustrates a cryptographic good practice where keying material and, in turn, keys are derived for a specific purpose using a label and a context as inputs to the KDF.

12.3.4 Derive-Secret

Finally, the TLS 1.3 Derive-Secret function DS is defined as shown in Figure 12.6. It takes a secret, a label, and TLS messages as input, and outputs one of the TLS secrets listed in Table 12.1. In the subsequent step, these secrets will be used to derive the TLS keys.

As a result, multiple calls to Derive-Secret can be used to derive keying material for different secret keys even with the same secret as input as long as different messages are used to compute the transcript hash.

Figure 12.6: The Derive-Secret function DS

Derive-Secret implements a clever way to bind the keying material to previous messages exchanged during a specific execution of a cryptographic protocol. This is desirable from a cryptography perspective because it causes Alice and Bob to derive completely different secret keys and, as a result, leads to a failure of the cryptographic protocol since Alice cannot understand what Bob encrypted or authenticated, and vice versa.

This approach implements an implicit protection against man-in-the-middle attacks. Even if Mallory manages to intercept and manipulate messages exchanged by Alice and Bob, she cannot trick them into deriving an identical secret key because Alice’s message transcript will be different from Bob’s message transcript.

As illustrated in Figure 12.7, Alice and Bob start by deriving the Early Secret SE and an intermediate secret S0 (which will be used for further computations). Eventually, Alice and Bob will establish a secure TLS channel by deriving the shared cryptographic keys from these secrets.

Figure 12.7: Derivation of the TLS early secret and first derived secret S0

If a specific TLS secret is not available, a zero value – a string of 0-valued bytes – is taken as input. As an example, if the pre-shared key PSK is not used, the early secret will be computed as follows:
Early_Secret = HKDF-Extract(0, 0)